Table of Contents
Pyramidal Harmonics
From the Tesseral Harmonics and for a given angular momentum $l$ one can construct an orbital basis where the basis orbitals have the same shape, but differ in orientation. This implies that this basis can be obtained by specifying one of these orbitals and obtain the others by rotating the first one. A possible realization is to align these orbitals along the slant edges of a pyramid with a regular polygon of order $2l+1$ as base [1,2]. Hence, the name “Pyramidal Harmonics”. Below we show these for $l=0...3$, but this can be done for every $l$. The first row depicts the view from the side, the second row depicts the view from the top along the z-axis.
$l = 0$

$l = 1$
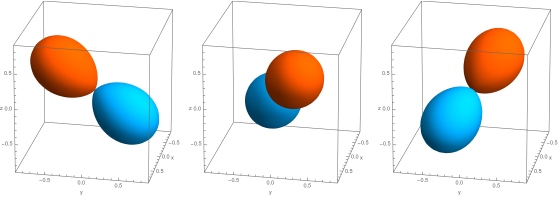
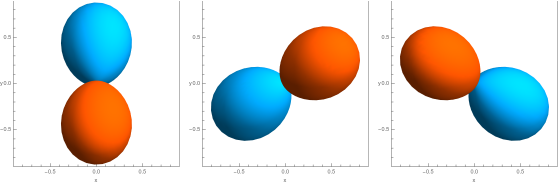
$l = 2$
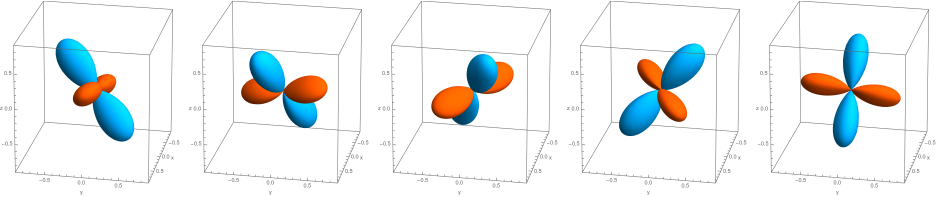

$l = 3$


Citations
[1] Kimball, G. E., J. Chem. Phys., 8, 188 (1940)
[2] Powell, R. E., J. Chem. Education, Vol. 45, 1 (1968)