Density matrix plot

An intuitive way to look at eigenstates is to plot the charge density. For multi-electron wave-functions one can not plot the wave-function (it depends on $3\times n$ coordinates) but the charge density is a well defined simple quantity. We here use the rendering options of \textit{Mathematica} in combination with the package for \textit{Mathematica} (Quanty.nb) to plot the density matrix of the lowest three eigenstates in NiO.

The input script is:

density_matrix_plots_Mathematica.Quanty

-- It is often nice to make plots of the resulting "wave-functions" Now one can not
-- simply plot a multi-electron wavefunction \psi(r_1,r_2,r_3, ..., r_n) as it depends
-- on 3n coordinates.
-- One can plot the resulting charge density.
 
-- This example calculates the density matrix of a state and then calls Mathematica to
-- make a density plot of this matrix.
 
-- the script for mathematica is included in the input file
-- the input string needs calculated data which will be substituted before calling mathematica
 
Verbosity(0)
 
-- You need to change the absolute path in the script below
mathematicaInput = [[
Needs["Quanty`PlotTools`"];
rho=%s;
pl = Table[ Rasterize[ DensityMatrixPlot[IdentityMatrix[10] - rho[ [i] ], PlotRange -> {{-0.4, 0.4}, {-0.4, 0.4}, {-0.4, 0.4}}] ], {i, 1, Length[rho]}];
For[i = 1, i <= Length[pl], i++,
    Export["/Users/haverkort/Documents/Quanty/Example_and_Testing/History/current/Tutorials/20_NiO_Crystal_Field/Rho" <> ToString[i] <> ".png", pl[ [i] ] ];
   ];
Quit[];
]]
 
NF=10
NB=0
dIndexDn={0,2,4,6,8}
dIndexUp={1,3,5,7,9}
 
OppSx   =NewOperator("Sx"   ,NF, dIndexUp, dIndexDn)
OppSy   =NewOperator("Sy"   ,NF, dIndexUp, dIndexDn)
OppSz   =NewOperator("Sz"   ,NF, dIndexUp, dIndexDn)
OppSsqr =NewOperator("Ssqr" ,NF, dIndexUp, dIndexDn)
OppSplus=NewOperator("Splus",NF, dIndexUp, dIndexDn)
OppSmin =NewOperator("Smin" ,NF, dIndexUp, dIndexDn)
 
OppLx   =NewOperator("Lx"   ,NF, dIndexUp, dIndexDn)
OppLy   =NewOperator("Ly"   ,NF, dIndexUp, dIndexDn)
OppLz   =NewOperator("Lz"   ,NF, dIndexUp, dIndexDn)
OppLsqr =NewOperator("Lsqr" ,NF, dIndexUp, dIndexDn)
OppLplus=NewOperator("Lplus",NF, dIndexUp, dIndexDn)
OppLmin =NewOperator("Lmin" ,NF, dIndexUp, dIndexDn)
 
OppJx   =NewOperator("Jx"   ,NF, dIndexUp, dIndexDn)
OppJy   =NewOperator("Jy"   ,NF, dIndexUp, dIndexDn)
OppJz   =NewOperator("Jz"   ,NF, dIndexUp, dIndexDn)
OppJsqr =NewOperator("Jsqr" ,NF, dIndexUp, dIndexDn)
OppJplus=NewOperator("Jplus",NF, dIndexUp, dIndexDn)
OppJmin =NewOperator("Jmin" ,NF, dIndexUp, dIndexDn)
 
Oppldots=NewOperator("ldots",NF, dIndexUp, dIndexDn)
 
-- define the coulomb operator
-- we here define the part depending on F0 seperately from the part depending on F2
-- when summing we can put in the numerical values of the slater integrals
OppF0 =NewOperator("U", NF, dIndexUp, dIndexDn, {1,0,0})
OppF2 =NewOperator("U", NF, dIndexUp, dIndexDn, {0,1,0})
OppF4 =NewOperator("U", NF, dIndexUp, dIndexDn, {0,0,1})
 
-- Akm = {{k1,m1,Akm1},{k2,m2,Akm2}, ... }
Akm = PotentialExpandedOnClm("Oh", 2, {0.6,-0.4})
OpptenDq = NewOperator("CF", NF, dIndexUp, dIndexDn, Akm)
 
Akm = PotentialExpandedOnClm("Oh", 2, {1,0})
OppNeg = NewOperator("CF", NF, dIndexUp, dIndexDn, Akm)
Akm = PotentialExpandedOnClm("Oh", 2, {0,1})
OppNt2g = NewOperator("CF", NF, dIndexUp, dIndexDn, Akm)
 
Hamiltonian =  10.0 * OppF2 + 6.25 * OppF4 + 2.0 * OpptenDq + 0.06 * Oppldots + 0.000001 * (2*OppSz + OppLz)
 
-- we now can create the lowest Npsi eigenstates:
Npsi=3
-- in order to make sure we have a filling of 2 electrons we need to define some restrictions
StartRestrictions = {NF, NB, {"1111111111",8,8}}
 
psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi)
oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSz, OppLz, Oppldots, OppF2, OppF4, OppNeg, OppNt2g}
 
print(" <E>    <S^2>  <L^2>  <J^2>  <S_z>  <L_z>  <l.s>  <F[2]> <F[4]> <Neg>  <Nt2g>");
for key,psi in pairs(psiList) do
  expvalue = psi * oppList * psi
  for k,v in pairs(expvalue) do
    io.write(string.format("%6.3f ",v))
  end;
  io.write("\n")
end
io:flush()
 
function tableToMathematica(t)
  local ret = "{ "
  for k,v in pairs(t) do
    if k~=1 then 
      ret = ret.." , "
    end
    if (type(v) == "table") then
      ret = ret..tableToMathematica(v)
    else
      ret = ret..string.format("%18.15f + (%18.15f) I ",Complex.Re(v),Complex.Im(v))
    end
  end
  ret = ret.." }"
  return ret
end
 
rhoList = DensityMatrix(psiList, {0,1,2,3,4,5,6,7,8,9})
rhoListMathematicaForm = tableToMathematica(rhoList)
 
file = io.open("densitymatrix.nb", "w")
file:write( mathematicaInput:format( rhoListMathematicaForm ) )
file:close()
 
os.execute("/Applications/Mathematica08.app/Contents/MacOS/MathKernel -run '<<densitymatrix.nb'")
os.execute("convert Rho1.png -transparent white temp.png ; convert temp.png Rho1.eps ; rm temp.png")
os.execute("convert Rho2.png -transparent white temp.png ; convert temp.png Rho2.eps ; rm temp.png")
os.execute("convert Rho3.png -transparent white temp.png ; convert temp.png Rho3.eps ; rm temp.png")

The produced figures are:

$S_z=-1$	$S_z=0$	$S_z=1$

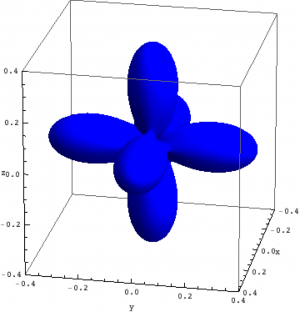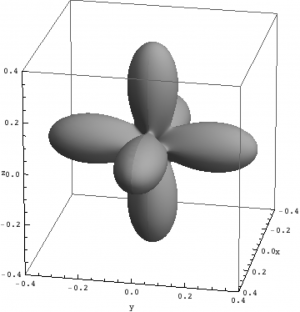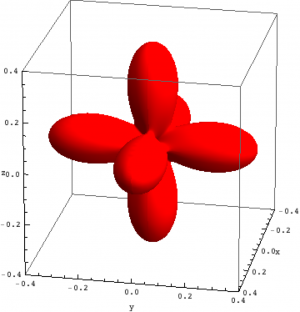Density matrix of the ground, first and second excited state of Ni in NiO.

The plots can be seen in the figure above. We show the hole density (identity matrix minus the density matrix) which has lobes towards the O atoms. Ni in NiO has a hole in the $x^2-y^2$ and in the $z^2$ orbital. The color represent the spin down, $S_z=0$ and spin up state of the lowest triplet.

The output to the screen is:

density_matrix_plots_Mathematica.out

 <E>    <S^2>  <L^2>  <J^2>  <S_z>  <L_z>  <l.s>  <F[2]> <F[4]> <Neg>  <Nt2g>
-18.093  2.000 12.000 14.471 -0.999 -0.119 -0.147 -1.020 -0.878  2.002  5.998 
-18.093  2.000 12.000 14.471 -0.000 -0.000 -0.147 -1.020 -0.878  2.002  5.998 
-18.093  2.000 12.000 14.471  0.999  0.119 -0.147 -1.020 -0.878  2.002  5.998 
Mathematica 8.0 for Mac OS X x86 (64-bit)
Copyright 1988-2011 Wolfram Research, Inc.
Loaded the Quanty : Plot Tools Package - version 2016.4.13
Written by Maurits W. Haverkort

Density matrix plot

Table of contents