Spherical Harmonic (Y)
Download a notebook that generates this page
The spherical harmonics are defined as $$ Y_l^{(m)} = \frac{\sqrt{2 l+1}}{2 \sqrt{\pi }} \sqrt{\frac{(l-m)!}{(l+m)!}} e^{i m \phi } P_l^{(m)}(\cos (\theta )), $$ with $l$ the angular momentum and $m$ the z projection of the angular momentum, $-l \leq m\leq l$. $P_l^{(m)}$ are the associated Legendre polynomials. For positive $m$ these are defined in terms of the unassociated Legendre polynomials as: $$ \begin{align} P_l^{(m)}(x) & = (-1)^m(1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x)\\ &= \frac{(-1)^m}{2^l l!}(1-x^2)^{m/2} \frac{d^{l+m}}{dx^{l+m}}(x^2-1)^l, \end{align} $$ using in the second line that: $$ P_l(x)=\frac{1}{2^l l!}\frac{d^l}{dx^l} (x^2-1)^l. $$ For negative $m$ the associated Legendre polynomials are defined as: $$ P_l^{(-m)}(x) = (-1)^m \frac{(l-m)!}{(l+m)!} P_l^{(m)}(x). $$ We thus include the Condon-Shortley phase $(-1)^m$ in our definitions of the associated Legendre polynomials.
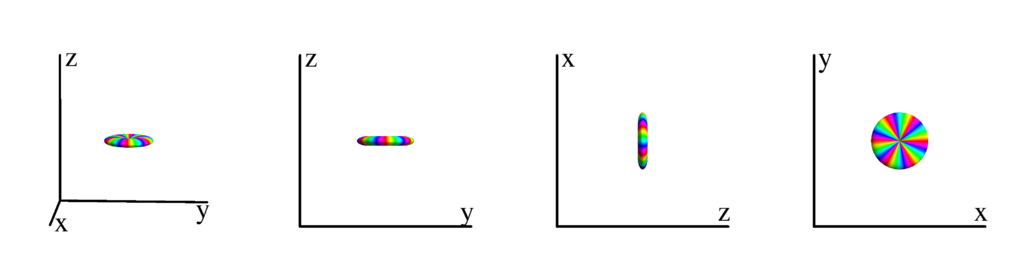
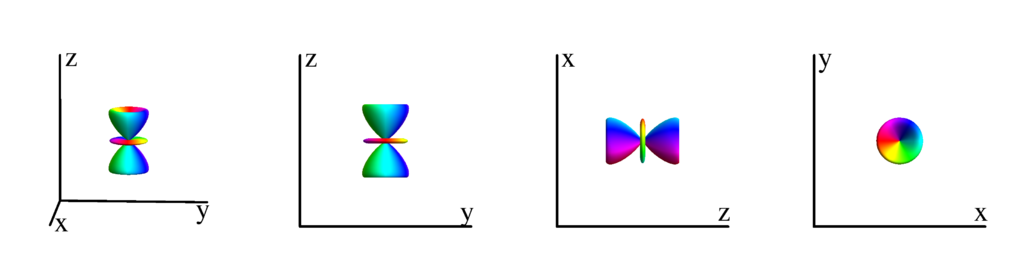
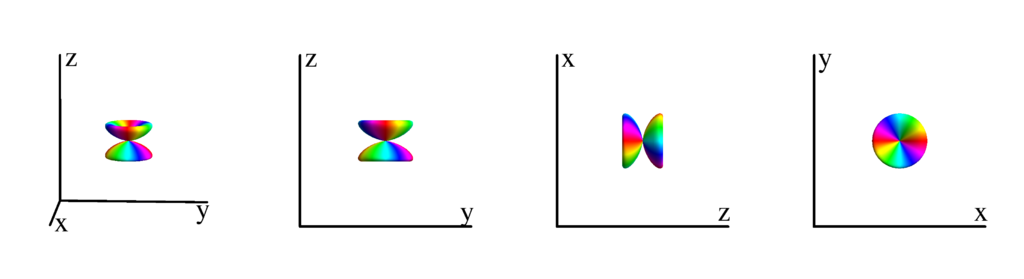
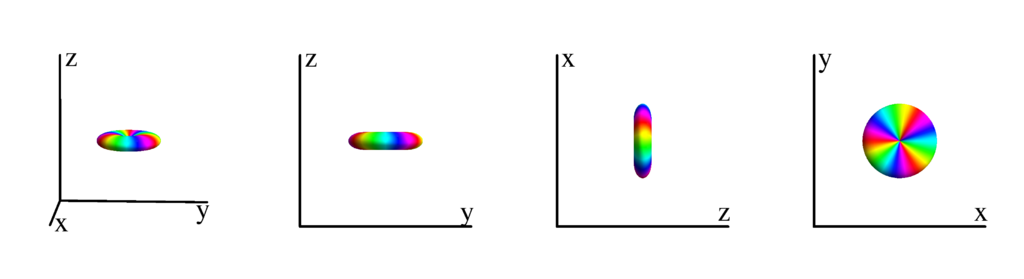
The following table shows the spherical harmonics up to $l=6$. We list both the explicit function in terms of the angular coordinates $\theta$ and $\phi$ as well as the function in terms of the directional cosines $x$, $y$ and $z$. Using a right hand coordinate system the relation is: $x=\cos(\phi)\sin(\theta)$, $y=\sin(\phi)\sin(\theta)$ and $z=\cos(\theta)$. The plots show the surface defined by the equation $r={Y_l^{(m)}}^* Y_l^{(m)}$. The color of the surface is according to the phase with red for positive, cyan for negative, a mixture of yellow and green for pure positive imaginary values and a mixture of blue and magenta for pure negative imaginary values. We show a 3D image as well as a projection along the $x$, $y$ and $z$ direction.
$l=0$
$m_l=0$
$$ Y_{0}^{(0)}=\frac{1}{2 \sqrt{\pi }}\\ \phantom{Y_{0}^{(0)}}=\frac{1}{2 \sqrt{\pi }} $$

$l=1$
$m_l=-1$
$$ Y_{1}^{(-1)}=\frac{1}{2} \sqrt{\frac{3}{2 \pi }} e^{-i \phi } \sin (\theta )\\ \phantom{Y_{1}^{(-1)}}=\frac{1}{2} \sqrt{\frac{3}{2 \pi }} (x-i y) $$
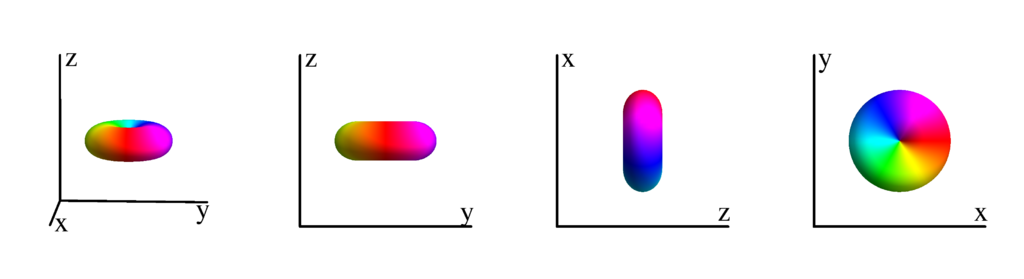
$m_l=0$
$$ Y_{1}^{(0)}=\frac{1}{2} \sqrt{\frac{3}{\pi }} \cos (\theta )\\ \phantom{Y_{1}^{(0)}}=\frac{1}{2} \sqrt{\frac{3}{\pi }} z $$
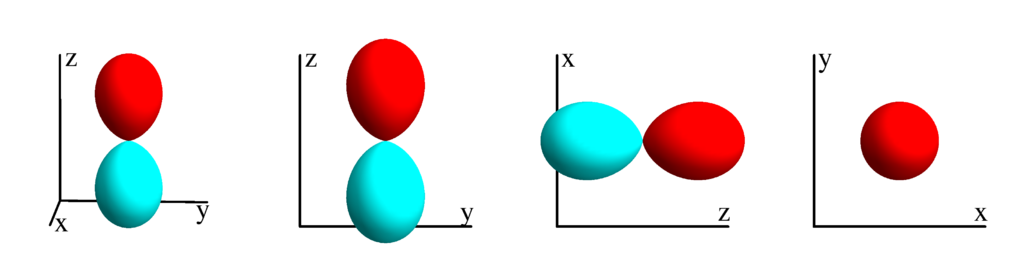
$m_l=1$
$$ Y_{1}^{(1)}=-\frac{1}{2} \sqrt{\frac{3}{2 \pi }} e^{i \phi } \sin (\theta )\\ \phantom{Y_{1}^{(1)}}=-\frac{1}{2} \sqrt{\frac{3}{2 \pi }} (x+i y) $$
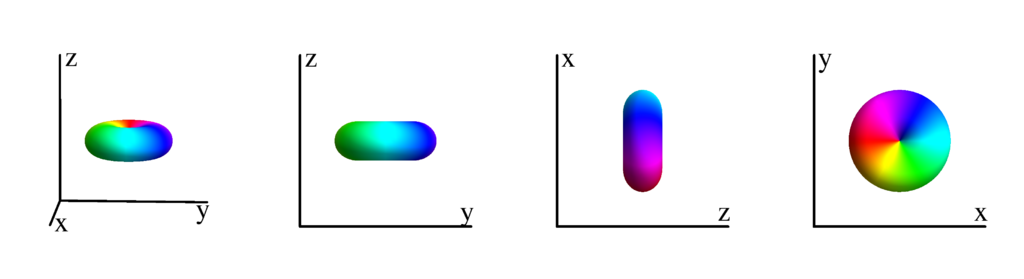
$l=2$
$m_l=-2$
$$ Y_{2}^{(-2)}=\frac{1}{4} \sqrt{\frac{15}{2 \pi }} e^{-2 i \phi } \sin ^2(\theta )\\ \phantom{Y_{2}^{(-2)}}=\frac{1}{4} \sqrt{\frac{15}{2 \pi }} (x-i y)^2 $$
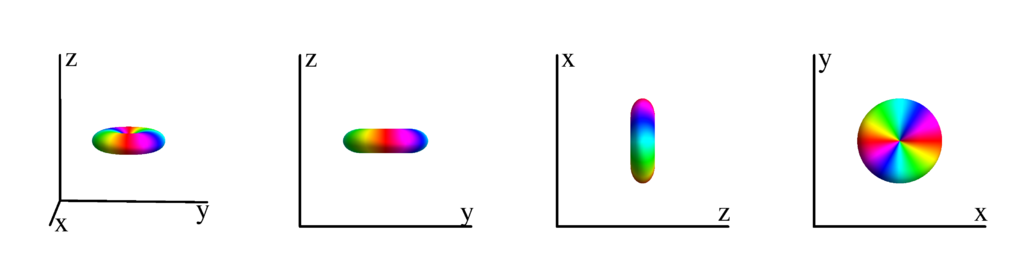
$m_l=-1$
$$ Y_{2}^{(-1)}=\frac{1}{2} \sqrt{\frac{15}{2 \pi }} e^{-i \phi } \sin (\theta ) \cos (\theta )\\ \phantom{Y_{2}^{(-1)}}=\frac{1}{2} \sqrt{\frac{15}{2 \pi }} z (x-i y) $$
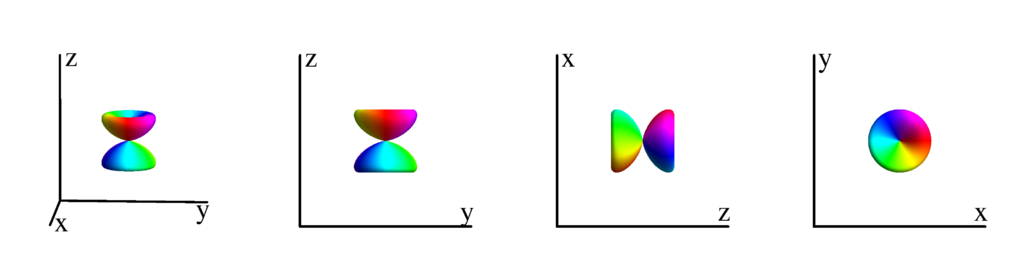
$m_l=0$
$$ Y_{2}^{(0)}=\frac{1}{4} \sqrt{\frac{5}{\pi }} \left(3 \cos ^2(\theta )-1\right)\\ \phantom{Y_{2}^{(0)}}=-\frac{1}{4} \sqrt{\frac{5}{\pi }} \left(x^2+y^2-2 z^2\right) $$
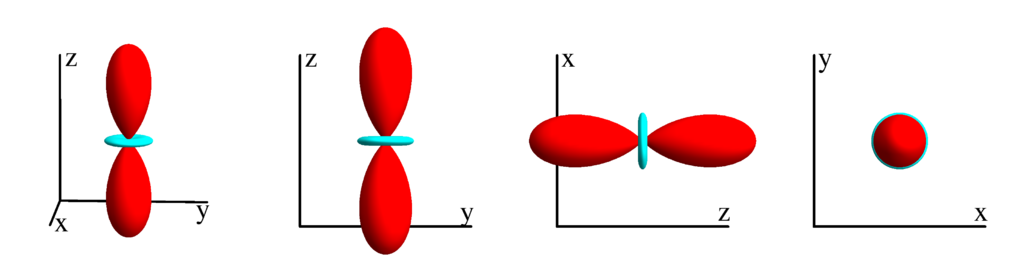
$m_l=1$
$$ Y_{2}^{(1)}=-\frac{1}{2} \sqrt{\frac{15}{2 \pi }} e^{i \phi } \sin (\theta ) \cos (\theta )\\ \phantom{Y_{2}^{(1)}}=-\frac{1}{2} \sqrt{\frac{15}{2 \pi }} z (x+i y) $$
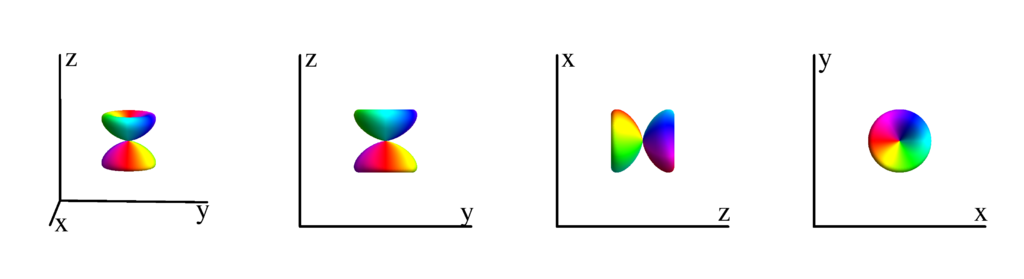
$m_l=2$
$$ Y_{2}^{(2)}=\frac{1}{4} \sqrt{\frac{15}{2 \pi }} e^{2 i \phi } \sin ^2(\theta )\\ \phantom{Y_{2}^{(2)}}=\frac{1}{4} \sqrt{\frac{15}{2 \pi }} (x+i y)^2 $$
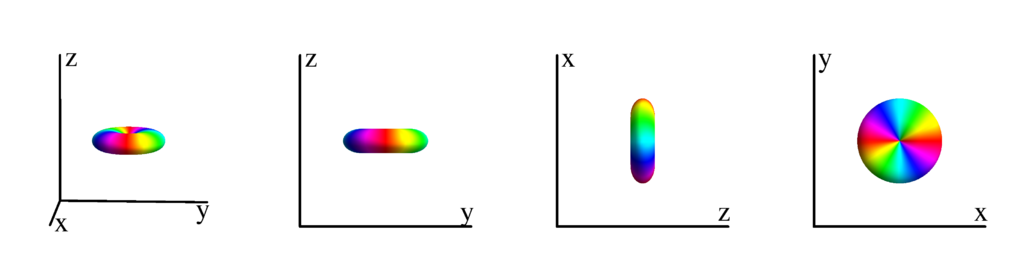
$l=3$
$m_l=-3$
$$ Y_{3}^{(-3)}=\frac{1}{8} \sqrt{\frac{35}{\pi }} e^{-3 i \phi } \sin ^3(\theta )\\ \phantom{Y_{3}^{(-3)}}=\frac{1}{8} \sqrt{\frac{35}{\pi }} (x-i y)^3 $$
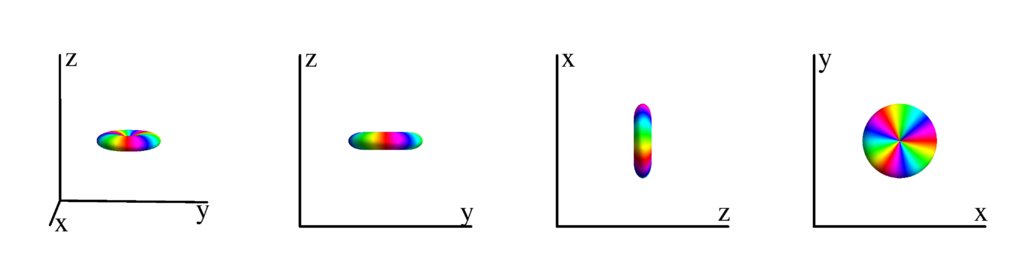
$m_l=-2$
$$ Y_{3}^{(-2)}=\frac{1}{4} \sqrt{\frac{105}{2 \pi }} e^{-2 i \phi } \sin ^2(\theta ) \cos (\theta )\\ \phantom{Y_{3}^{(-2)}}=\frac{1}{4} \sqrt{\frac{105}{2 \pi }} z (x-i y)^2 $$
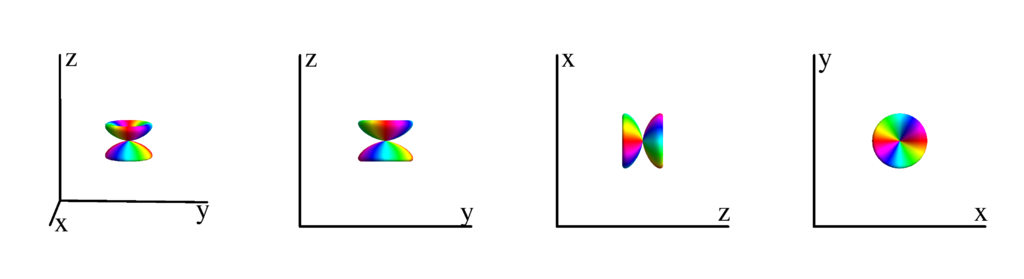
$m_l=-1$
$$ Y_{3}^{(-1)}=\frac{1}{8} \sqrt{\frac{21}{\pi }} e^{-i \phi } \sin (\theta ) \left(5 \cos ^2(\theta )-1\right)\\ \phantom{Y_{3}^{(-1)}}=-\frac{1}{8} \sqrt{\frac{21}{\pi }} (x-i y) \left(x^2+y^2-4 z^2\right) $$
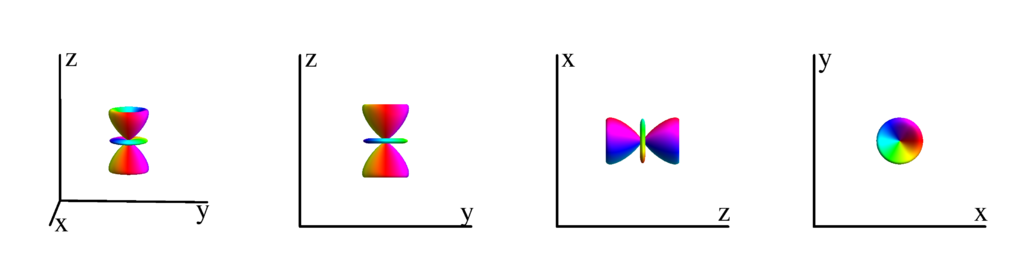
$m_l=0$
$$ Y_{3}^{(0)}=\frac{1}{4} \sqrt{\frac{7}{\pi }} \left(5 \cos ^3(\theta )-3 \cos (\theta )\right)\\ \phantom{Y_{3}^{(0)}}=\frac{1}{4} \sqrt{\frac{7}{\pi }} z \left(2 z^2-3 \left(x^2+y^2\right)\right) $$
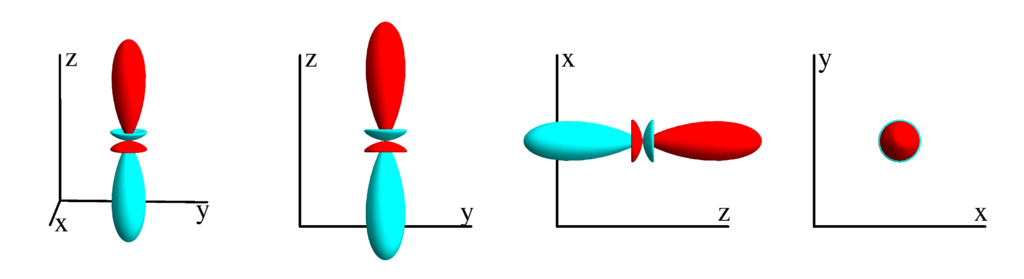
$m_l=1$
$$ Y_{3}^{(1)}=-\frac{1}{8} \sqrt{\frac{21}{\pi }} e^{i \phi } \sin (\theta ) \left(5 \cos ^2(\theta )-1\right)\\ \phantom{Y_{3}^{(1)}}=\frac{1}{8} \sqrt{\frac{21}{\pi }} (x+i y) \left(x^2+y^2-4 z^2\right) $$
$m_l=2$
$$ Y_{3}^{(2)}=\frac{1}{4} \sqrt{\frac{105}{2 \pi }} e^{2 i \phi } \sin ^2(\theta ) \cos (\theta )\\ \phantom{Y_{3}^{(2)}}=\frac{1}{4} \sqrt{\frac{105}{2 \pi }} z (x+i y)^2 $$
$m_l=3$
$$ Y_{3}^{(3)}=-\frac{1}{8} \sqrt{\frac{35}{\pi }} e^{3 i \phi } \sin ^3(\theta )\\ \phantom{Y_{3}^{(3)}}=-\frac{1}{8} \sqrt{\frac{35}{\pi }} (x+i y)^3 $$
$l=4$
$m_l=-4$
$$ Y_{4}^{(-4)}=\frac{3}{16} \sqrt{\frac{35}{2 \pi }} e^{-4 i \phi } \sin ^4(\theta )\\ \phantom{Y_{4}^{(-4)}}=\frac{3}{16} \sqrt{\frac{35}{2 \pi }} (x-i y)^4 $$
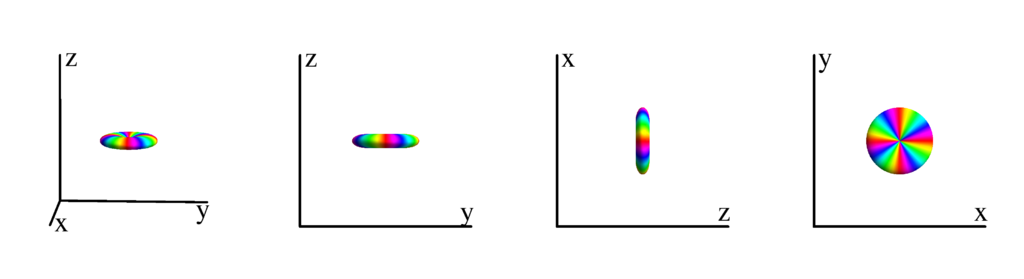
$m_l=-3$
$$ Y_{4}^{(-3)}=\frac{3}{8} \sqrt{\frac{35}{\pi }} e^{-3 i \phi } \sin ^3(\theta ) \cos (\theta )\\ \phantom{Y_{4}^{(-3)}}=\frac{3}{8} \sqrt{\frac{35}{\pi }} z (x-i y)^3 $$
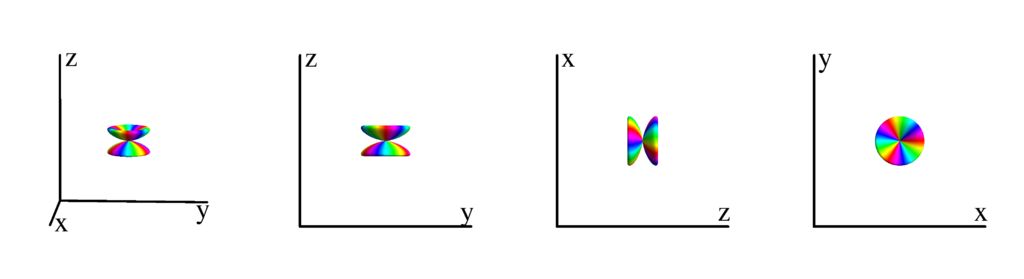
$m_l=-2$
$$ Y_{4}^{(-2)}=\frac{3}{8} \sqrt{\frac{5}{2 \pi }} e^{-2 i \phi } \sin ^2(\theta ) \left(7 \cos ^2(\theta )-1\right)\\ \phantom{Y_{4}^{(-2)}}=-\frac{3}{8} \sqrt{\frac{5}{2 \pi }} (x-i y)^2 \left(x^2+y^2-6 z^2\right) $$
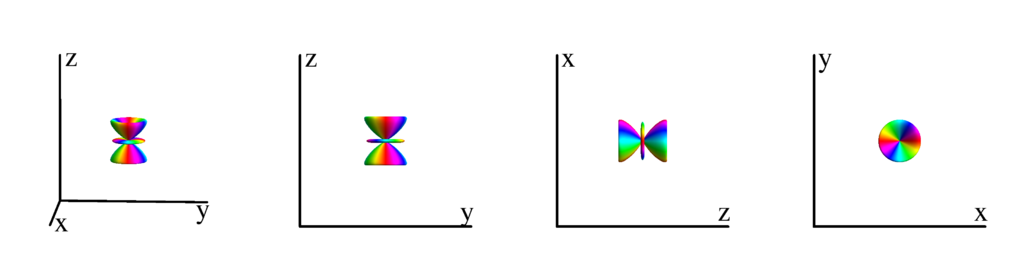
$m_l=-1$
$$ Y_{4}^{(-1)}=\frac{3}{8} \sqrt{\frac{5}{\pi }} e^{-i \phi } \sin (\theta ) \cos (\theta ) \left(7 \cos ^2(\theta )-3\right)\\ \phantom{Y_{4}^{(-1)}}=-\frac{3}{8} \sqrt{\frac{5}{\pi }} z (x-i y) \left(3 \left(x^2+y^2\right)-4 z^2\right) $$
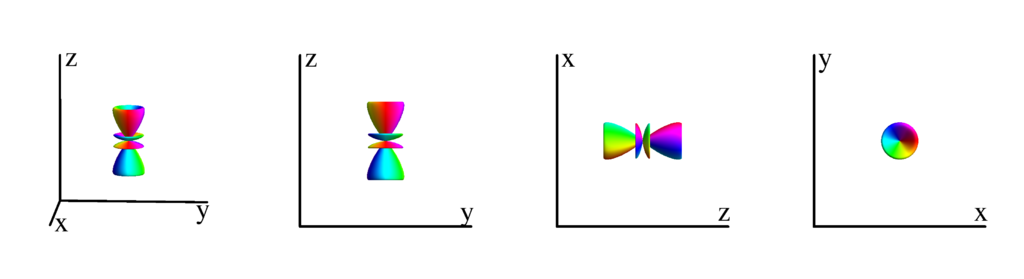
$m_l=0$
$$ Y_{4}^{(0)}=\frac{3 \left(35 \cos ^4(\theta )-30 \cos ^2(\theta )+3\right)}{16 \sqrt{\pi }}\\ \phantom{Y_{4}^{(0)}}=\frac{-72 z^2 \left(x^2+y^2\right)+9 \left(x^2+y^2\right)^2+24 z^4}{16 \sqrt{\pi }} $$
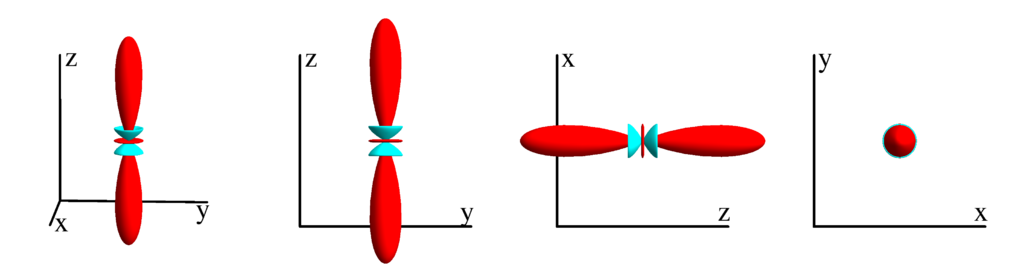
$m_l=1$
$$ Y_{4}^{(1)}=-\frac{3}{8} \sqrt{\frac{5}{\pi }} e^{i \phi } \sin (\theta ) \cos (\theta ) \left(7 \cos ^2(\theta )-3\right)\\ \phantom{Y_{4}^{(1)}}=\frac{3}{8} \sqrt{\frac{5}{\pi }} z (x+i y) \left(3 \left(x^2+y^2\right)-4 z^2\right) $$
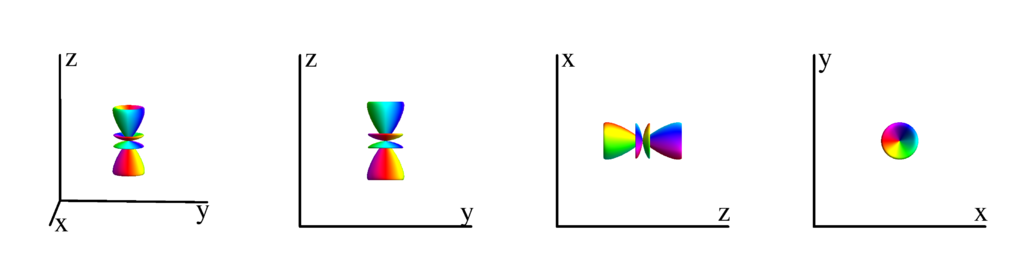
$m_l=2$
$$ Y_{4}^{(2)}=\frac{3}{8} \sqrt{\frac{5}{2 \pi }} e^{2 i \phi } \sin ^2(\theta ) \left(7 \cos ^2(\theta )-1\right)\\ \phantom{Y_{4}^{(2)}}=-\frac{3}{8} \sqrt{\frac{5}{2 \pi }} (x+i y)^2 \left(x^2+y^2-6 z^2\right) $$
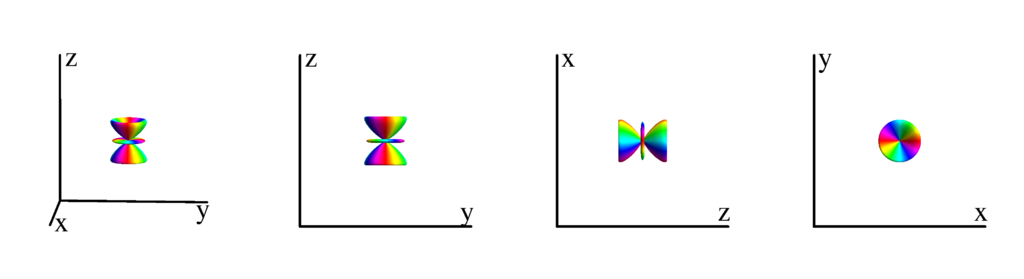
$m_l=3$
$$ Y_{4}^{(3)}=-\frac{3}{8} \sqrt{\frac{35}{\pi }} e^{3 i \phi } \sin ^3(\theta ) \cos (\theta )\\ \phantom{Y_{4}^{(3)}}=-\frac{3}{8} \sqrt{\frac{35}{\pi }} z (x+i y)^3 $$
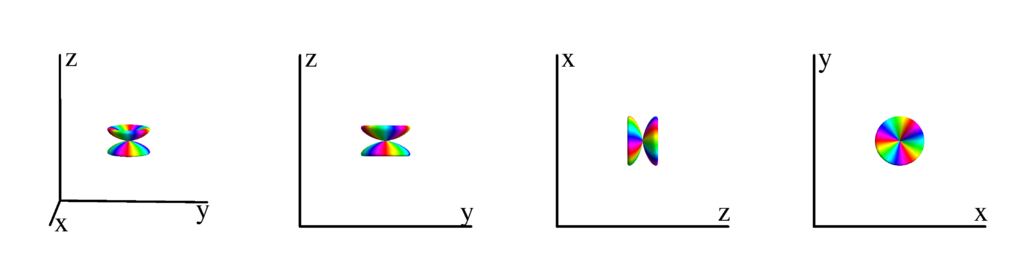
$m_l=4$
$$ Y_{4}^{(4)}=\frac{3}{16} \sqrt{\frac{35}{2 \pi }} e^{4 i \phi } \sin ^4(\theta )\\ \phantom{Y_{4}^{(4)}}=\frac{3}{16} \sqrt{\frac{35}{2 \pi }} (x+i y)^4 $$

$l=5$
$m_l=-5$
$$ Y_{5}^{(-5)}=\frac{3}{32} \sqrt{\frac{77}{\pi }} e^{-5 i \phi } \sin ^5(\theta )\\ \phantom{Y_{5}^{(-5)}}=\frac{3}{32} \sqrt{\frac{77}{\pi }} (x-i y)^5 $$
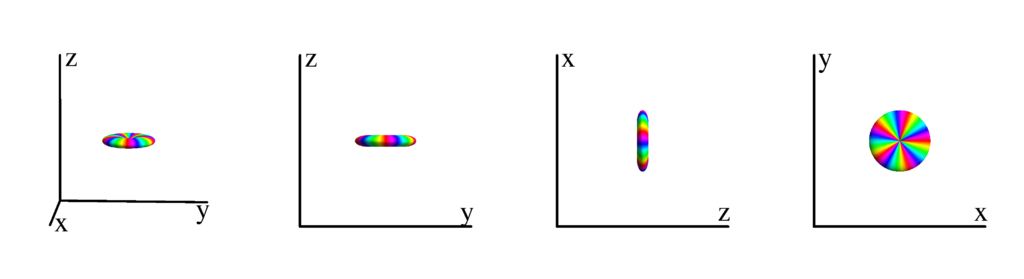
$m_l=-4$
$$ Y_{5}^{(-4)}=\frac{3}{16} \sqrt{\frac{385}{2 \pi }} e^{-4 i \phi } \sin ^4(\theta ) \cos (\theta )\\ \phantom{Y_{5}^{(-4)}}=\frac{3}{16} \sqrt{\frac{385}{2 \pi }} z (x-i y)^4 $$
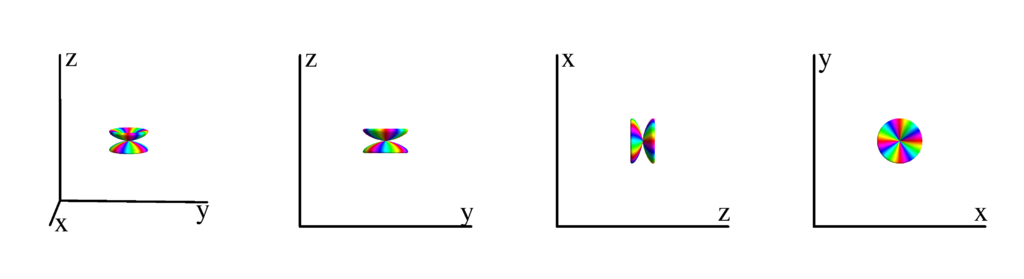
$m_l=-3$
$$ Y_{5}^{(-3)}=\frac{1}{32} \sqrt{\frac{385}{\pi }} e^{-3 i \phi } \sin ^3(\theta ) \left(9 \cos ^2(\theta )-1\right)\\ \phantom{Y_{5}^{(-3)}}=-\frac{1}{32} \sqrt{\frac{385}{\pi }} (x-i y)^3 \left(x^2+y^2-8 z^2\right) $$
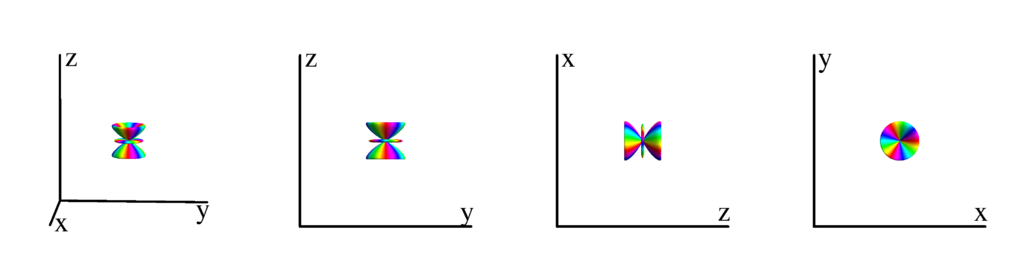
$m_l=-2$
$$ Y_{5}^{(-2)}=\frac{1}{8} \sqrt{\frac{1155}{2 \pi }} e^{-2 i \phi } \sin ^2(\theta ) \cos (\theta ) \left(3 \cos ^2(\theta )-1\right)\\ \phantom{Y_{5}^{(-2)}}=-\frac{1}{8} \sqrt{\frac{1155}{2 \pi }} z (x-i y)^2 \left(x^2+y^2-2 z^2\right) $$
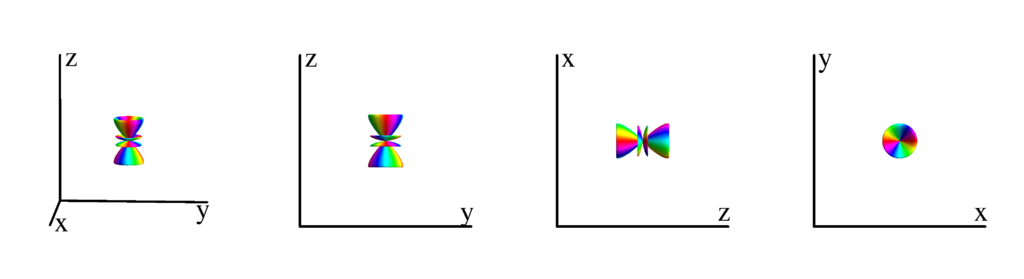
$m_l=-1$
$$ Y_{5}^{(-1)}=\frac{1}{16} \sqrt{\frac{165}{2 \pi }} e^{-i \phi } \sin (\theta ) \left(21 \cos ^4(\theta )-14 \cos ^2(\theta )+1\right)\\ \phantom{Y_{5}^{(-1)}}=\frac{1}{16} \sqrt{\frac{165}{2 \pi }} (x-i y) \left(-12 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+8 z^4\right) $$
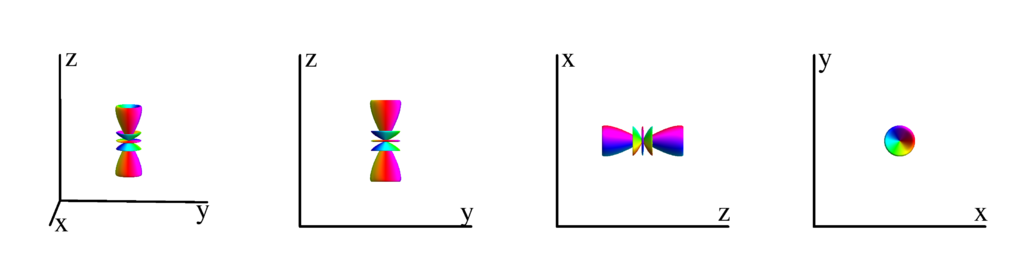
$m_l=0$
$$ Y_{5}^{(0)}=\frac{1}{16} \sqrt{\frac{11}{\pi }} \left(63 \cos ^5(\theta )-70 \cos ^3(\theta )+15 \cos (\theta )\right)\\ \phantom{Y_{5}^{(0)}}=\frac{1}{16} \sqrt{\frac{11}{\pi }} z \left(-40 z^2 \left(x^2+y^2\right)+15 \left(x^2+y^2\right)^2+8 z^4\right) $$
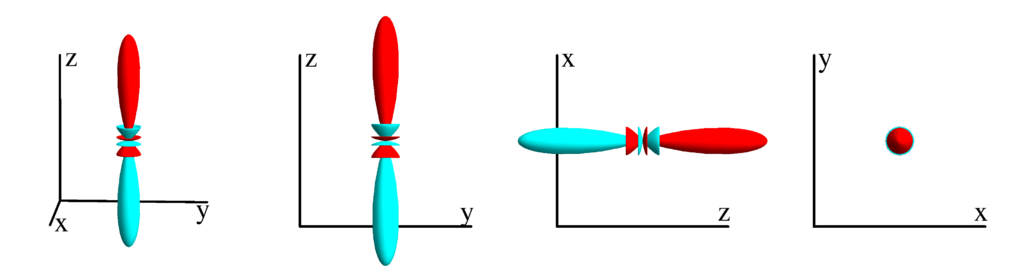
$m_l=1$
$$ Y_{5}^{(1)}=-\frac{1}{16} \sqrt{\frac{165}{2 \pi }} e^{i \phi } \sin (\theta ) \left(21 \cos ^4(\theta )-14 \cos ^2(\theta )+1\right)\\ \phantom{Y_{5}^{(1)}}=-\frac{1}{16} \sqrt{\frac{165}{2 \pi }} (x+i y) \left(-12 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+8 z^4\right) $$
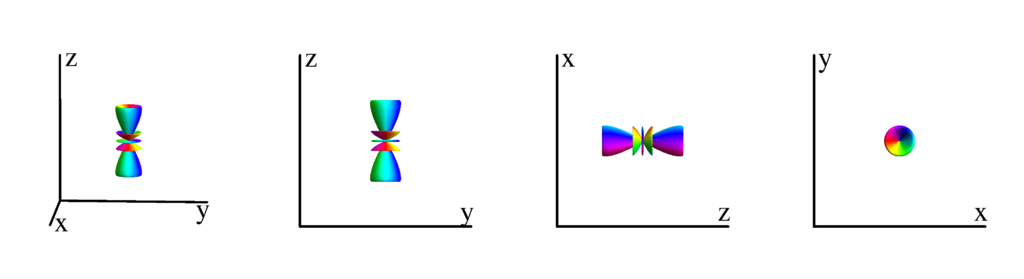
$m_l=2$
$$ Y_{5}^{(2)}=\frac{1}{8} \sqrt{\frac{1155}{2 \pi }} e^{2 i \phi } \sin ^2(\theta ) \cos (\theta ) \left(3 \cos ^2(\theta )-1\right)\\ \phantom{Y_{5}^{(2)}}=-\frac{1}{8} \sqrt{\frac{1155}{2 \pi }} z (x+i y)^2 \left(x^2+y^2-2 z^2\right) $$
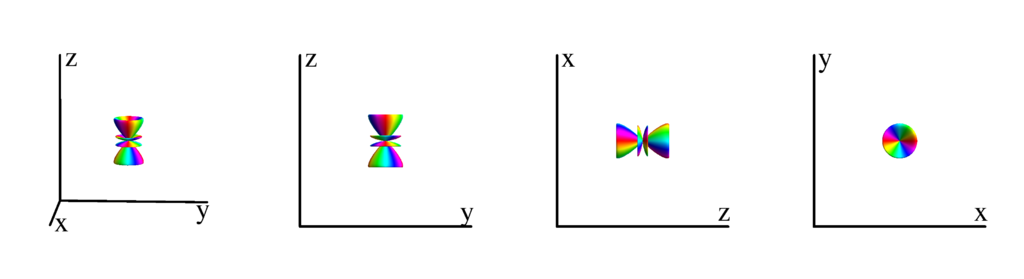
$m_l=3$
$$ Y_{5}^{(3)}=-\frac{1}{32} \sqrt{\frac{385}{\pi }} e^{3 i \phi } \sin ^3(\theta ) \left(9 \cos ^2(\theta )-1\right)\\ \phantom{Y_{5}^{(3)}}=\frac{1}{32} \sqrt{\frac{385}{\pi }} (x+i y)^3 \left(x^2+y^2-8 z^2\right) $$
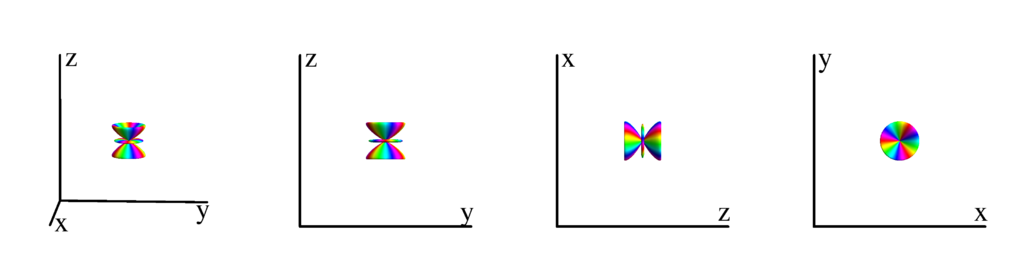
$m_l=4$
$$ Y_{5}^{(4)}=\frac{3}{16} \sqrt{\frac{385}{2 \pi }} e^{4 i \phi } \sin ^4(\theta ) \cos (\theta )\\ \phantom{Y_{5}^{(4)}}=\frac{3}{16} \sqrt{\frac{385}{2 \pi }} z (x+i y)^4 $$
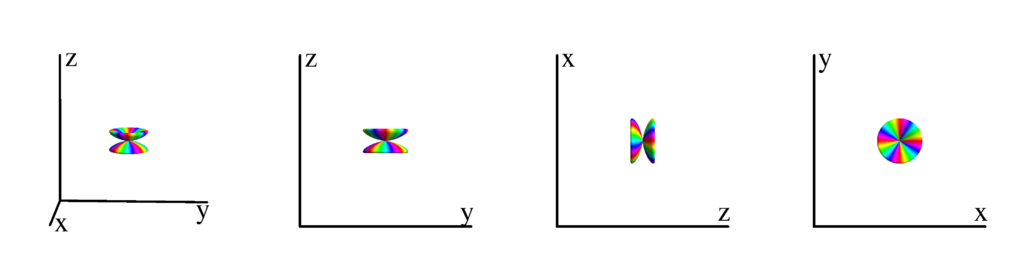
$m_l=5$
$$ Y_{5}^{(5)}=-\frac{3}{32} \sqrt{\frac{77}{\pi }} e^{5 i \phi } \sin ^5(\theta )\\ \phantom{Y_{5}^{(5)}}=-\frac{3}{32} \sqrt{\frac{77}{\pi }} (x+i y)^5 $$
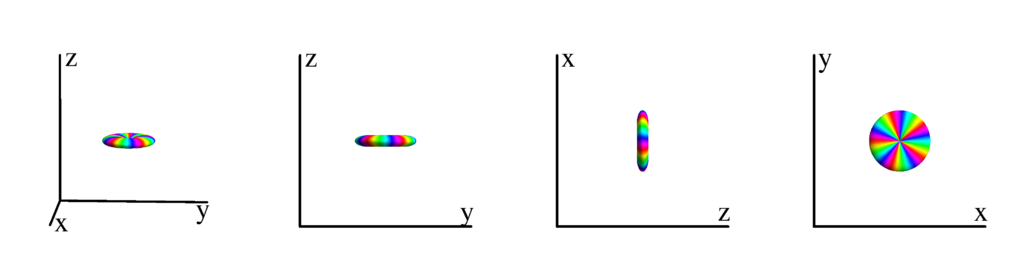
$l=6$
$m_l=-6$
$$ Y_{6}^{(-6)}=\frac{1}{64} \sqrt{\frac{3003}{\pi }} e^{-6 i \phi } \sin ^6(\theta )\\ \phantom{Y_{6}^{(-6)}}=\frac{1}{64} \sqrt{\frac{3003}{\pi }} (x-i y)^6 $$
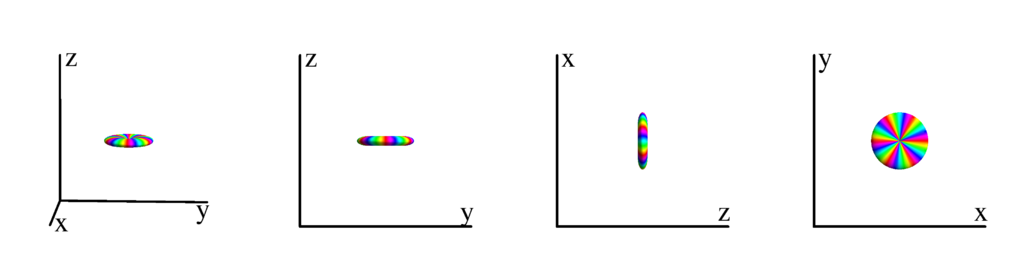
$m_l=-5$
$$ Y_{6}^{(-5)}=\frac{3}{32} \sqrt{\frac{1001}{\pi }} e^{-5 i \phi } \sin ^5(\theta ) \cos (\theta )\\ \phantom{Y_{6}^{(-5)}}=\frac{3}{32} \sqrt{\frac{1001}{\pi }} z (x-i y)^5 $$
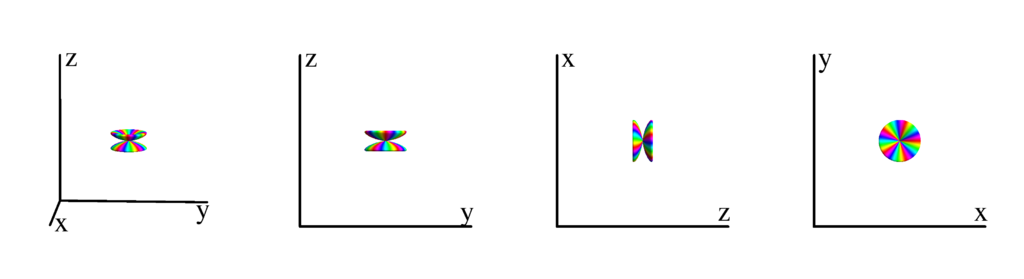
$m_l=-4$
$$ Y_{6}^{(-4)}=\frac{3}{32} \sqrt{\frac{91}{2 \pi }} e^{-4 i \phi } \sin ^4(\theta ) \left(11 \cos ^2(\theta )-1\right)\\ \phantom{Y_{6}^{(-4)}}=-\frac{3}{32} \sqrt{\frac{91}{2 \pi }} (x-i y)^4 \left(x^2+y^2-10 z^2\right) $$
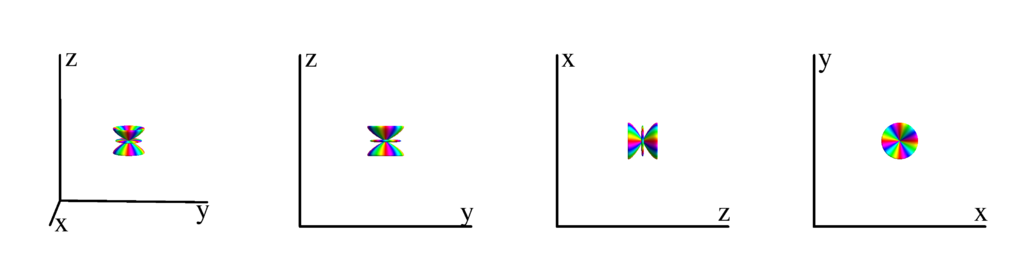
$m_l=-3$
$$ Y_{6}^{(-3)}=\frac{1}{32} \sqrt{\frac{1365}{\pi }} e^{-3 i \phi } \sin ^3(\theta ) \cos (\theta ) \left(11 \cos ^2(\theta )-3\right)\\ \phantom{Y_{6}^{(-3)}}=-\frac{1}{32} \sqrt{\frac{1365}{\pi }} z (x-i y)^3 \left(3 \left(x^2+y^2\right)-8 z^2\right) $$
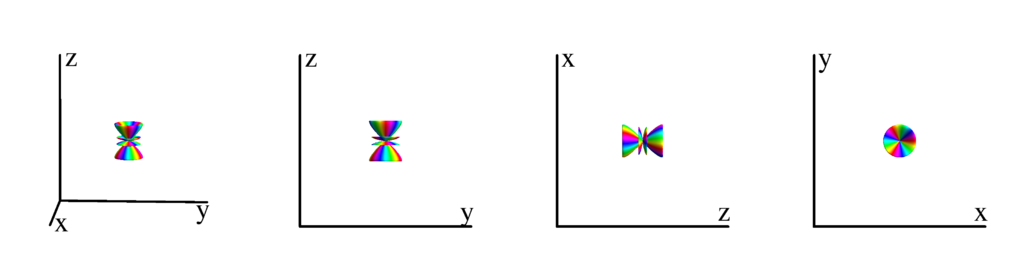
$m_l=-2$
$$ Y_{6}^{(-2)}=\frac{1}{64} \sqrt{\frac{1365}{\pi }} e^{-2 i \phi } \sin ^2(\theta ) \left(33 \cos ^4(\theta )-18 \cos ^2(\theta )+1\right)\\ \phantom{Y_{6}^{(-2)}}=\frac{1}{64} \sqrt{\frac{1365}{\pi }} (x-i y)^2 \left(-16 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+16 z^4\right) $$

$m_l=-1$
$$ Y_{6}^{(-1)}=\frac{1}{16} \sqrt{\frac{273}{2 \pi }} e^{-i \phi } \sin (\theta ) \cos (\theta ) \left(33 \cos ^4(\theta )-30 \cos ^2(\theta )+5\right)\\ \phantom{Y_{6}^{(-1)}}=\frac{1}{16} \sqrt{\frac{273}{2 \pi }} z (x-i y) \left(-20 z^2 \left(x^2+y^2\right)+5 \left(x^2+y^2\right)^2+8 z^4\right) $$
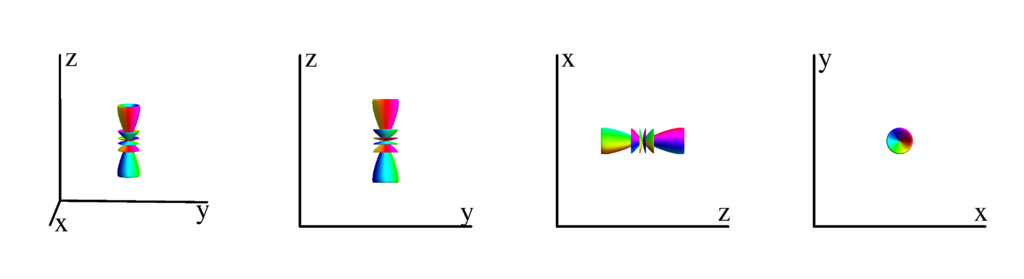
$m_l=0$
$$ Y_{6}^{(0)}=\frac{1}{32} \sqrt{\frac{13}{\pi }} \left(231 \cos ^6(\theta )-315 \cos ^4(\theta )+105 \cos ^2(\theta )-5\right)\\ \phantom{Y_{6}^{(0)}}=\frac{1}{32} \sqrt{\frac{13}{\pi }} \left(-120 z^4 \left(x^2+y^2\right)+90 z^2 \left(x^2+y^2\right)^2-5 \left(x^2+y^2\right)^3+16 z^6\right) $$

$m_l=1$
$$ Y_{6}^{(1)}=-\frac{1}{16} \sqrt{\frac{273}{2 \pi }} e^{i \phi } \sin (\theta ) \cos (\theta ) \left(33 \cos ^4(\theta )-30 \cos ^2(\theta )+5\right)\\ \phantom{Y_{6}^{(1)}}=-\frac{1}{16} \sqrt{\frac{273}{2 \pi }} z (x+i y) \left(-20 z^2 \left(x^2+y^2\right)+5 \left(x^2+y^2\right)^2+8 z^4\right) $$
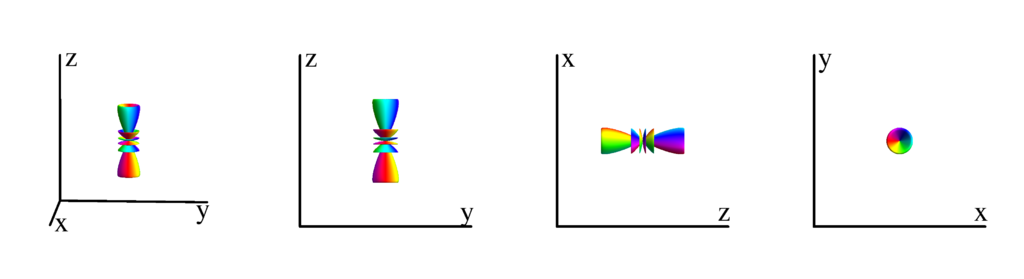
$m_l=2$
$$ Y_{6}^{(2)}=\frac{1}{64} \sqrt{\frac{1365}{\pi }} e^{2 i \phi } \sin ^2(\theta ) \left(33 \cos ^4(\theta )-18 \cos ^2(\theta )+1\right)\\ \phantom{Y_{6}^{(2)}}=\frac{1}{64} \sqrt{\frac{1365}{\pi }} (x+i y)^2 \left(-16 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+16 z^4\right) $$
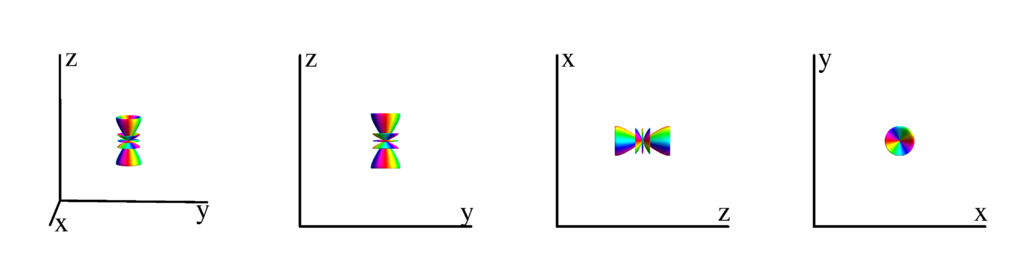
$m_l=3$
$$ Y_{6}^{(3)}=-\frac{1}{32} \sqrt{\frac{1365}{\pi }} e^{3 i \phi } \sin ^3(\theta ) \cos (\theta ) \left(11 \cos ^2(\theta )-3\right)\\ \phantom{Y_{6}^{(3)}}=\frac{1}{32} \sqrt{\frac{1365}{\pi }} z (x+i y)^3 \left(3 \left(x^2+y^2\right)-8 z^2\right) $$
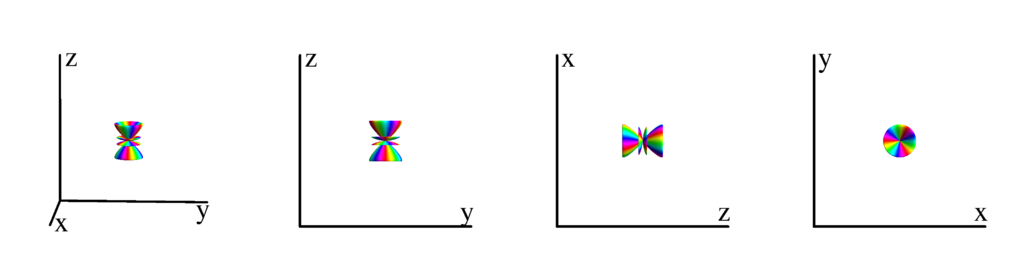
$m_l=4$
$$ Y_{6}^{(4)}=\frac{3}{32} \sqrt{\frac{91}{2 \pi }} e^{4 i \phi } \sin ^4(\theta ) \left(11 \cos ^2(\theta )-1\right)\\ \phantom{Y_{6}^{(4)}}=-\frac{3}{32} \sqrt{\frac{91}{2 \pi }} (x+i y)^4 \left(x^2+y^2-10 z^2\right) $$
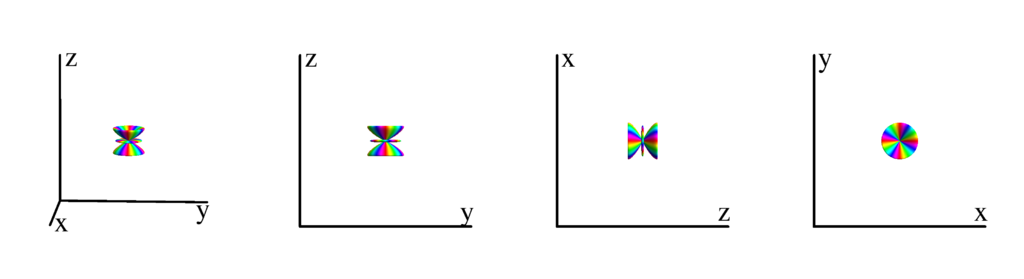
$m_l=5$
$$ Y_{6}^{(5)}=-\frac{3}{32} \sqrt{\frac{1001}{\pi }} e^{5 i \phi } \sin ^5(\theta ) \cos (\theta )\\ \phantom{Y_{6}^{(5)}}=-\frac{3}{32} \sqrt{\frac{1001}{\pi }} z (x+i y)^5 $$
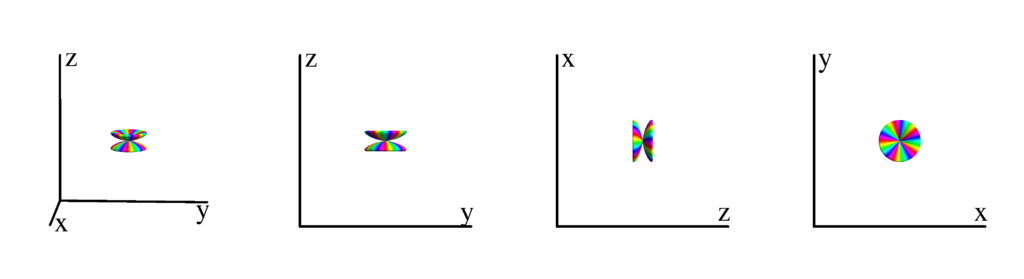
$m_l=6$
$$ Y_{6}^{(6)}=\frac{1}{64} \sqrt{\frac{3003}{\pi }} e^{6 i \phi } \sin ^6(\theta )\\ \phantom{Y_{6}^{(6)}}=\frac{1}{64} \sqrt{\frac{3003}{\pi }} (x+i y)^6 $$