This is an old revision of the document!
Tesseral Harmonics (Z)
Download a notebook that generates this page
The spherical harmonics are complex functions. For many cases one does not need to work with complex numbers and by making a suitable linear combination of the complex orbitals one can get a real basis. The tesseral harmonics are linear combinations of the spherical harmonics with $+m$ and $-m$ such that the result is a pure real function. For $m>0$ the tesseral harmonics have a $\cos(m\phi)$ dependence, for $m<0$ they have a $\sin(m\phi)$ dependence. The tesseral harmonics are defined as: $$ Z_l^{(m)}=\left\{\begin{array}{ll} Y_l^{(0)} & m=0\\ \frac{1}{\sqrt{2}} ( Y_l^{(-m)} + (-1)^m Y_l^{( m)} ) & m>0\\ \frac{\mathrm{i}}{\sqrt{2}} ( Y_l^{( m)} - (-1)^m Y_l^{(-m)} ) & m<0 \end{array}\right. $$
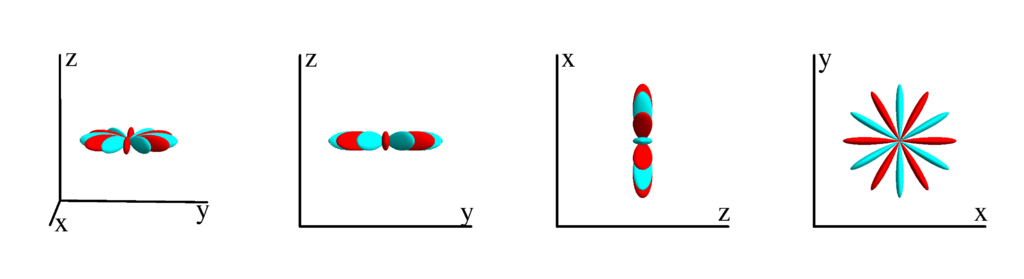
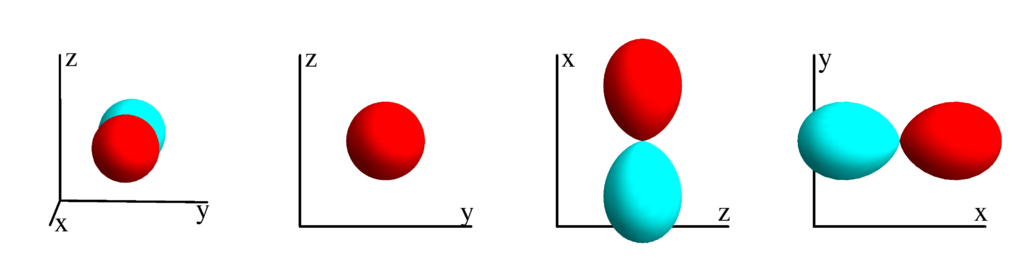
The following table shows the tesseral harmonics up to $l=6$. We list the explicit function in terms of the directional cosines $x$, $y$ and $z$. The plots show the surface defined by the equation $r={Z_l^{(m)}}^* Z_l^{(m)}$. The color of the surface is according to the phase with red for positive and cyan for negative. We show a 3D image as well as a projection along the $x$, $y$ and $z$ direction.
$l=0$
$m_l=0$
$$ Z_{0}^{(0)}=\frac{1}{2 \sqrt{\pi }}\\ \phantom{Z_{0}^{(0)}}=\frac{1}{2 \sqrt{\pi }} $$

$l=1$
$m_l=-1$
$$ Z_{1}^{(-1)}=\frac{1}{2} \sqrt{\frac{3}{\pi }} \sin (\theta ) \sin (\phi )\\ \phantom{Z_{1}^{(-1)}}=\frac{1}{2} \sqrt{\frac{3}{\pi }} y $$
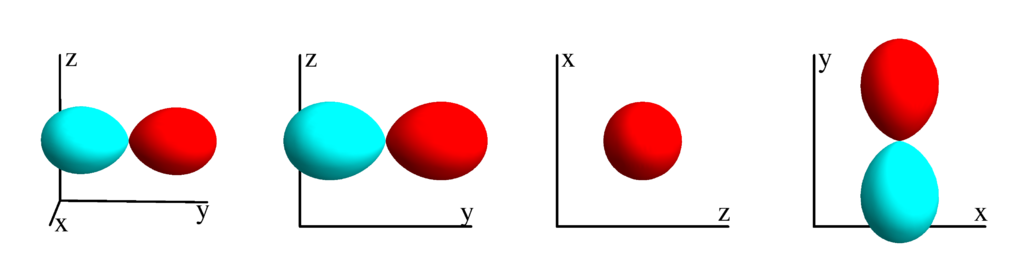
$m_l=0$
$$ Z_{1}^{(0)}=\frac{1}{2} \sqrt{\frac{3}{\pi }} \cos (\theta )\\ \phantom{Z_{1}^{(0)}}=\frac{1}{2} \sqrt{\frac{3}{\pi }} z $$
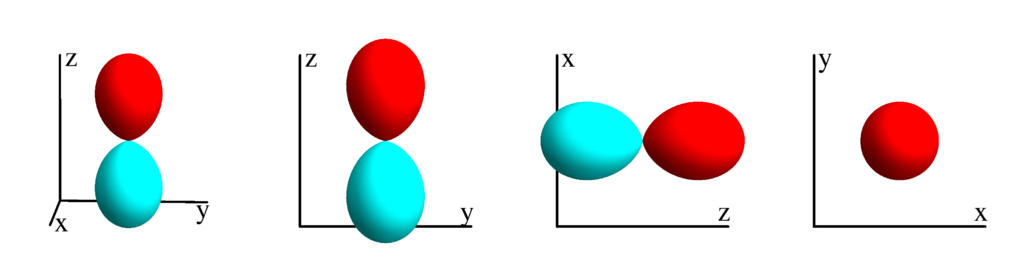
$m_l=1$
$$ Z_{1}^{(1)}=\frac{1}{2} \sqrt{\frac{3}{\pi }} \sin (\theta ) \cos (\phi )\\ \phantom{Z_{1}^{(1)}}=\frac{1}{2} \sqrt{\frac{3}{\pi }} x $$
$l=2$
$m_l=-2$
$$ Z_{2}^{(-2)}=\frac{1}{4} \sqrt{\frac{15}{\pi }} \sin ^2(\theta ) \sin (2 \phi )\\ \phantom{Z_{2}^{(-2)}}=\frac{1}{2} \sqrt{\frac{15}{\pi }} x y $$
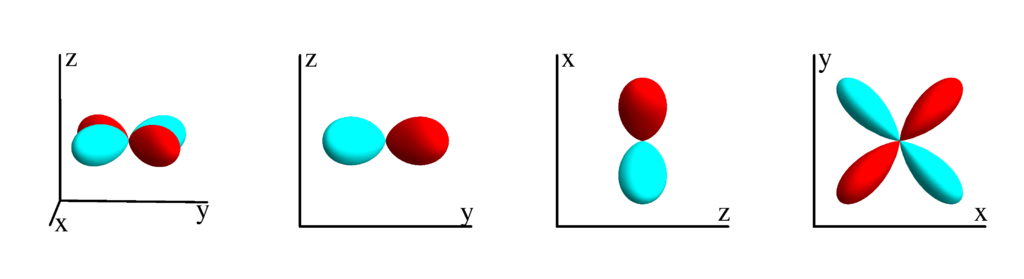
$m_l=-1$
$$ Z_{2}^{(-1)}=\frac{1}{2} \sqrt{\frac{15}{\pi }} \sin (\theta ) \cos (\theta ) \sin (\phi )\\ \phantom{Z_{2}^{(-1)}}=\frac{1}{2} \sqrt{\frac{15}{\pi }} y z $$
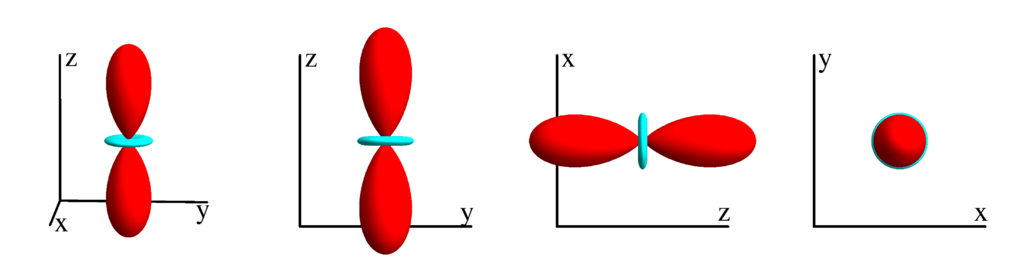
$m_l=0$
$$ Z_{2}^{(0)}=\frac{1}{8} \sqrt{\frac{5}{\pi }} (3 \cos (2 \theta )+1)\\ \phantom{Z_{2}^{(0)}}=-\frac{1}{4} \sqrt{\frac{5}{\pi }} \left(x^2+y^2-2 z^2\right) $$
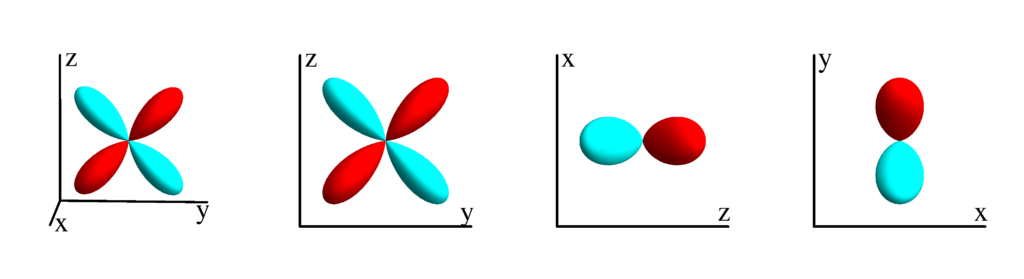
$m_l=1$
$$ Z_{2}^{(1)}=\frac{1}{2} \sqrt{\frac{15}{\pi }} \sin (\theta ) \cos (\theta ) \cos (\phi )\\ \phantom{Z_{2}^{(1)}}=\frac{1}{2} \sqrt{\frac{15}{\pi }} x z $$
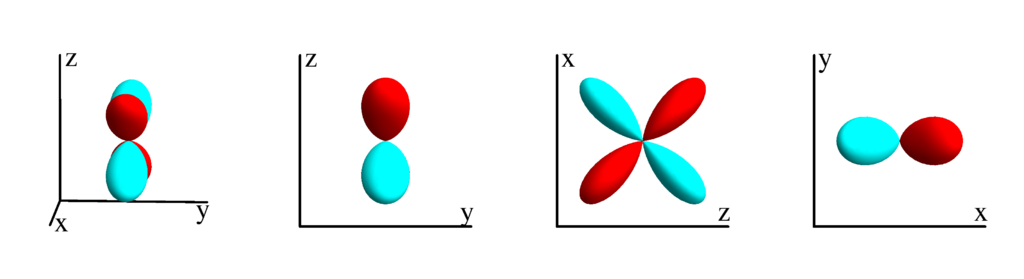
$m_l=2$
$$ Z_{2}^{(2)}=\frac{1}{4} \sqrt{\frac{15}{\pi }} \sin ^2(\theta ) \cos (2 \phi )\\ \phantom{Z_{2}^{(2)}}=\frac{1}{4} \sqrt{\frac{15}{\pi }} (x-y) (x+y) $$
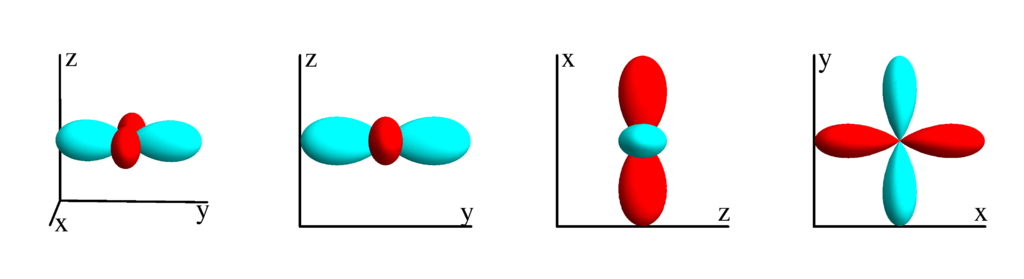
$l=3$
$m_l=-3$
$$ Z_{3}^{(-3)}=\frac{1}{4} \sqrt{\frac{35}{2 \pi }} \sin ^3(\theta ) \sin (3 \phi )\\ \phantom{Z_{3}^{(-3)}}=-\frac{1}{4} \sqrt{\frac{35}{2 \pi }} y \left(y^2-3 x^2\right) $$
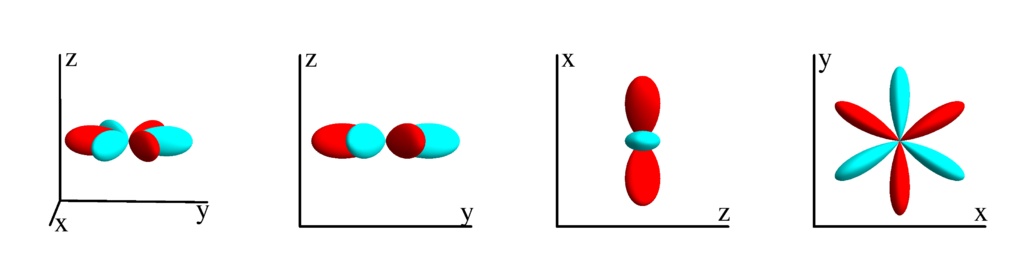
$m_l=-2$
$$ Z_{3}^{(-2)}=\frac{1}{4} \sqrt{\frac{105}{\pi }} \sin ^2(\theta ) \cos (\theta ) \sin (2 \phi )\\ \phantom{Z_{3}^{(-2)}}=\frac{1}{2} \sqrt{\frac{105}{\pi }} x y z $$
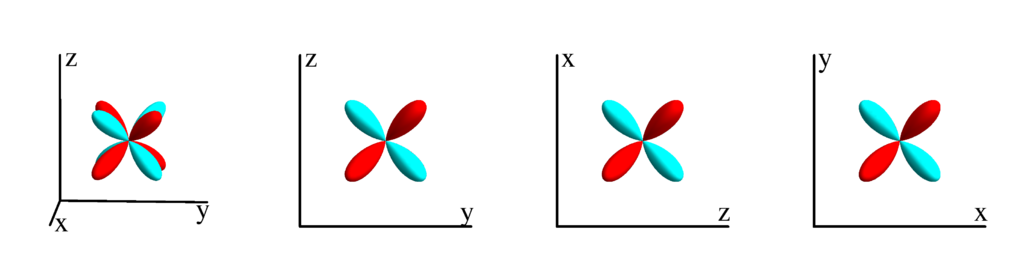
$m_l=-1$
$$ Z_{3}^{(-1)}=\frac{1}{16} \sqrt{\frac{21}{2 \pi }} (\sin (\theta )+5 \sin (3 \theta )) \sin (\phi )\\ \phantom{Z_{3}^{(-1)}}=-\frac{1}{4} \sqrt{\frac{21}{2 \pi }} y \left(x^2+y^2-4 z^2\right) $$
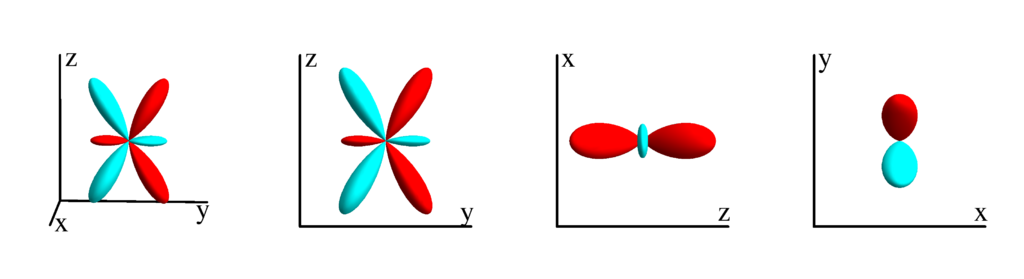
$m_l=0$
$$ Z_{3}^{(0)}=\frac{1}{8} \sqrt{\frac{7}{\pi }} \cos (\theta ) (5 \cos (2 \theta )-1)\\ \phantom{Z_{3}^{(0)}}=\frac{1}{4} \sqrt{\frac{7}{\pi }} z \left(2 z^2-3 \left(x^2+y^2\right)\right) $$
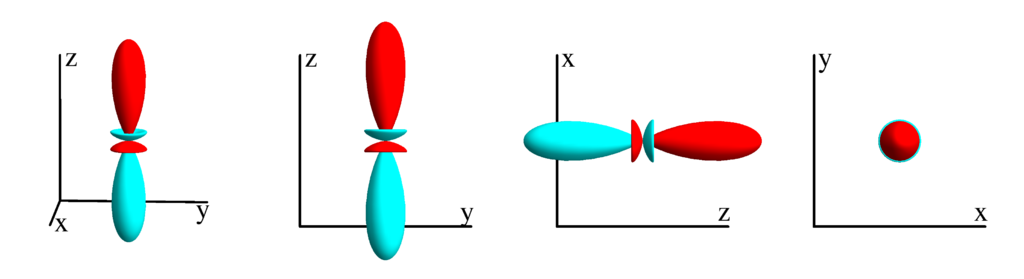
$m_l=1$
$$ Z_{3}^{(1)}=\frac{1}{16} \sqrt{\frac{21}{2 \pi }} (\sin (\theta )+5 \sin (3 \theta )) \cos (\phi )\\ \phantom{Z_{3}^{(1)}}=-\frac{1}{4} \sqrt{\frac{21}{2 \pi }} x \left(x^2+y^2-4 z^2\right) $$
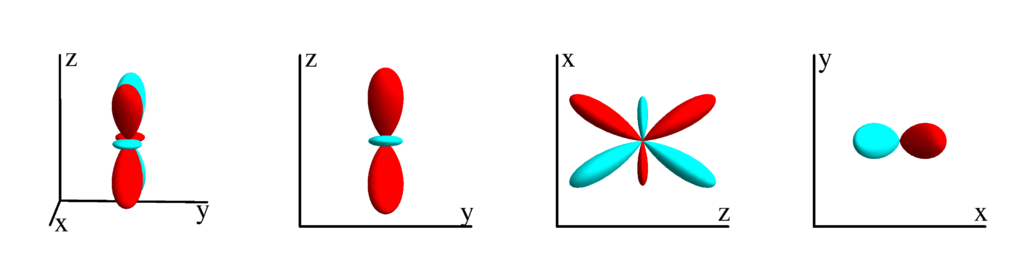
$m_l=2$
$$ Z_{3}^{(2)}=\frac{1}{4} \sqrt{\frac{105}{\pi }} \sin ^2(\theta ) \cos (\theta ) \cos (2 \phi )\\ \phantom{Z_{3}^{(2)}}=\frac{1}{4} \sqrt{\frac{105}{\pi }} z (x-y) (x+y) $$
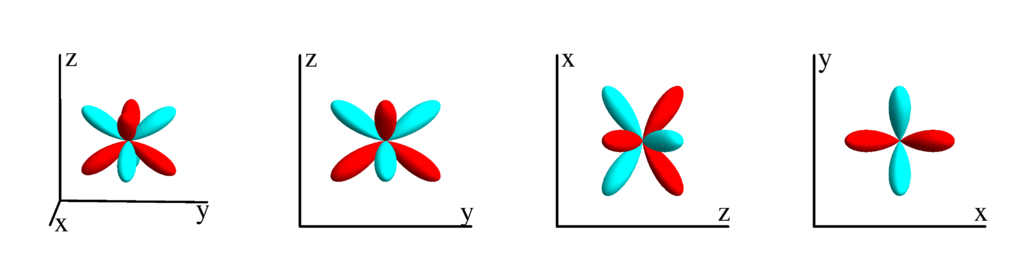
$m_l=3$
$$ Z_{3}^{(3)}=\frac{1}{4} \sqrt{\frac{35}{2 \pi }} \sin ^3(\theta ) \cos (3 \phi )\\ \phantom{Z_{3}^{(3)}}=\frac{1}{4} \sqrt{\frac{35}{2 \pi }} x \left(x^2-3 y^2\right) $$
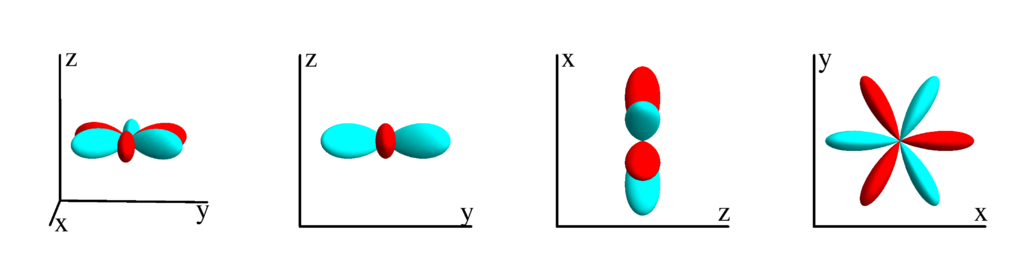
$l=4$
$m_l=-4$
$$ Z_{4}^{(-4)}=\frac{3}{16} \sqrt{\frac{35}{\pi }} \sin ^4(\theta ) \sin (4 \phi )\\ \phantom{Z_{4}^{(-4)}}=\frac{3}{4} \sqrt{\frac{35}{\pi }} x y (x-y) (x+y) $$
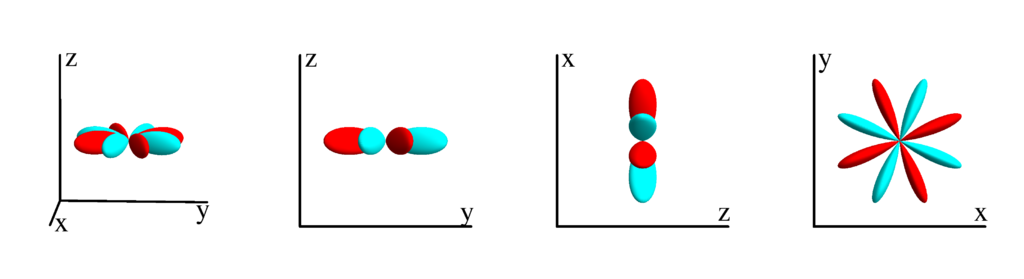
$m_l=-3$
$$ Z_{4}^{(-3)}=\frac{3}{4} \sqrt{\frac{35}{2 \pi }} \sin ^3(\theta ) \cos (\theta ) \sin (3 \phi )\\ \phantom{Z_{4}^{(-3)}}=-\frac{3}{4} \sqrt{\frac{35}{2 \pi }} y z \left(y^2-3 x^2\right) $$

$m_l=-2$
$$ Z_{4}^{(-2)}=\frac{3}{16} \sqrt{\frac{5}{\pi }} \sin ^2(\theta ) (7 \cos (2 \theta )+5) \sin (2 \phi )\\ \phantom{Z_{4}^{(-2)}}=-\frac{3}{4} \sqrt{\frac{5}{\pi }} x y \left(x^2+y^2-6 z^2\right) $$
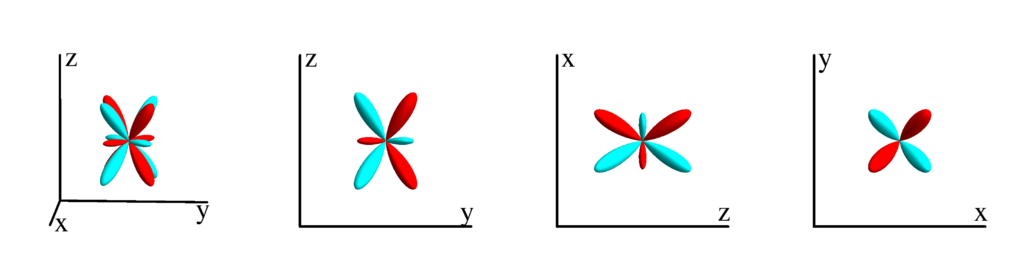
$m_l=-1$
$$ Z_{4}^{(-1)}=\frac{3}{32} \sqrt{\frac{5}{2 \pi }} (2 \sin (2 \theta )+7 \sin (4 \theta )) \sin (\phi )\\ \phantom{Z_{4}^{(-1)}}=-\frac{3}{4} \sqrt{\frac{5}{2 \pi }} y z \left(3 \left(x^2+y^2\right)-4 z^2\right) $$
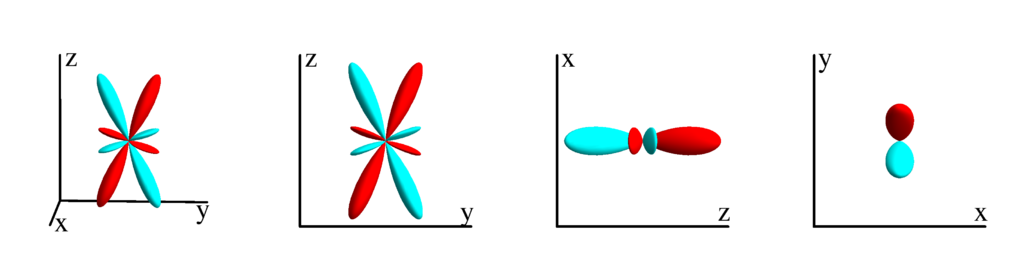
$m_l=0$
$$ Z_{4}^{(0)}=\frac{3 (20 \cos (2 \theta )+35 \cos (4 \theta )+9)}{128 \sqrt{\pi }}\\ \phantom{Z_{4}^{(0)}}=\frac{-72 z^2 \left(x^2+y^2\right)+9 \left(x^2+y^2\right)^2+24 z^4}{16 \sqrt{\pi }} $$
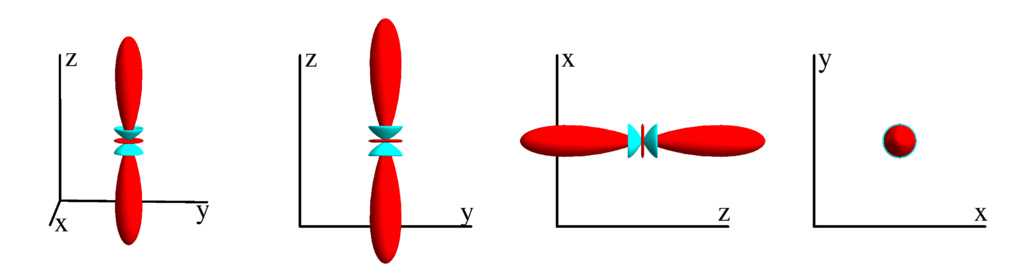
$m_l=1$
$$ Z_{4}^{(1)}=\frac{3}{32} \sqrt{\frac{5}{2 \pi }} (2 \sin (2 \theta )+7 \sin (4 \theta )) \cos (\phi )\\ \phantom{Z_{4}^{(1)}}=-\frac{3}{4} \sqrt{\frac{5}{2 \pi }} x z \left(3 \left(x^2+y^2\right)-4 z^2\right) $$
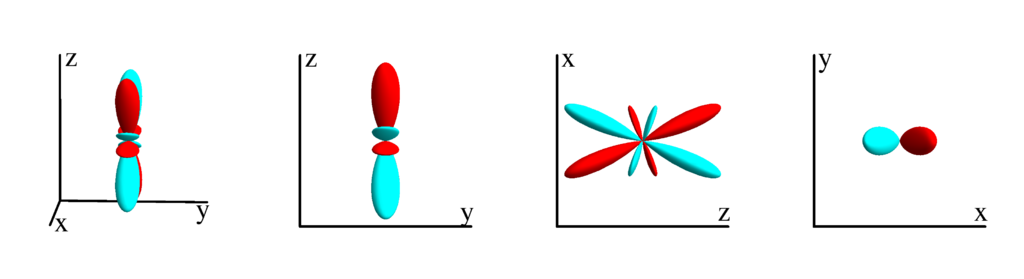
$m_l=2$
$$ Z_{4}^{(2)}=\frac{3}{16} \sqrt{\frac{5}{\pi }} \sin ^2(\theta ) (7 \cos (2 \theta )+5) \cos (2 \phi )\\ \phantom{Z_{4}^{(2)}}=-\frac{3}{8} \sqrt{\frac{5}{\pi }} (x-y) (x+y) \left(x^2+y^2-6 z^2\right) $$
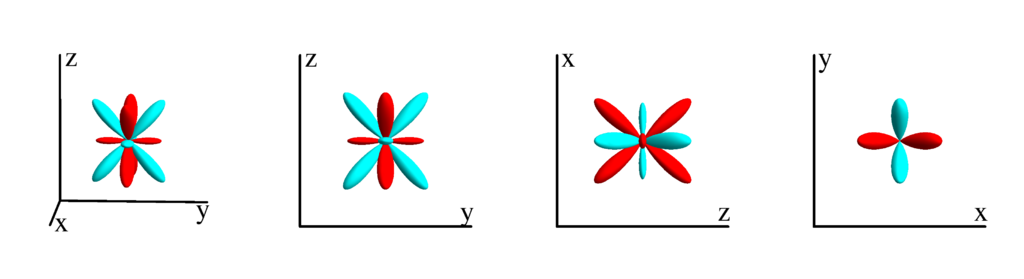
$m_l=3$
$$ Z_{4}^{(3)}=\frac{3}{4} \sqrt{\frac{35}{2 \pi }} \sin ^3(\theta ) \cos (\theta ) \cos (3 \phi )\\ \phantom{Z_{4}^{(3)}}=\frac{3}{4} \sqrt{\frac{35}{2 \pi }} x z \left(x^2-3 y^2\right) $$
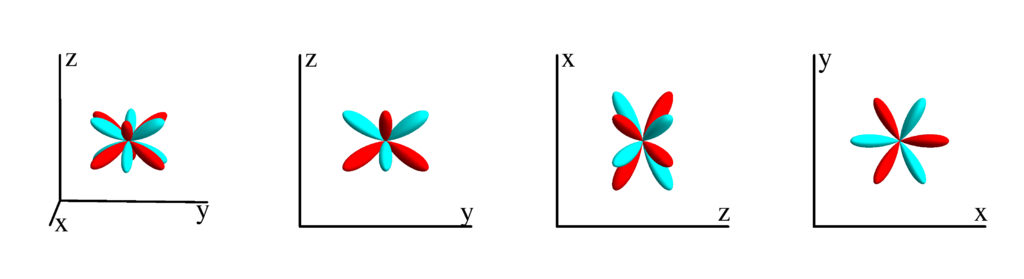
$m_l=4$
$$ Z_{4}^{(4)}=\frac{3}{16} \sqrt{\frac{35}{\pi }} \sin ^4(\theta ) \cos (4 \phi )\\ \phantom{Z_{4}^{(4)}}=\frac{3}{16} \sqrt{\frac{35}{\pi }} \left(x^4-6 x^2 y^2+y^4\right) $$
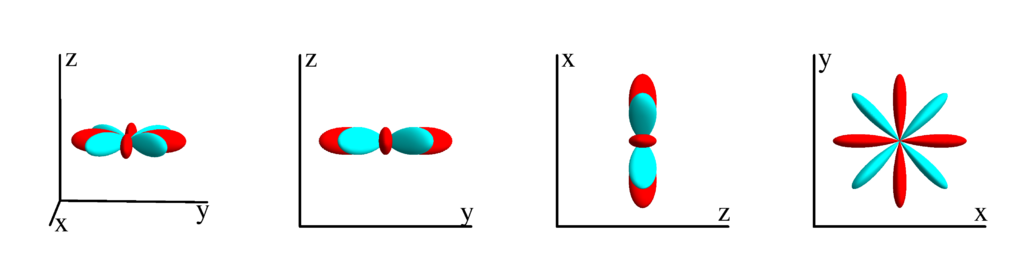
$l=5$
$m_l=-5$
$$ Z_{5}^{(-5)}=\frac{3}{16} \sqrt{\frac{77}{2 \pi }} \sin ^5(\theta ) \sin (5 \phi )\\ \phantom{Z_{5}^{(-5)}}=\frac{3}{16} \sqrt{\frac{77}{2 \pi }} y \left(5 x^4-10 x^2 y^2+y^4\right) $$
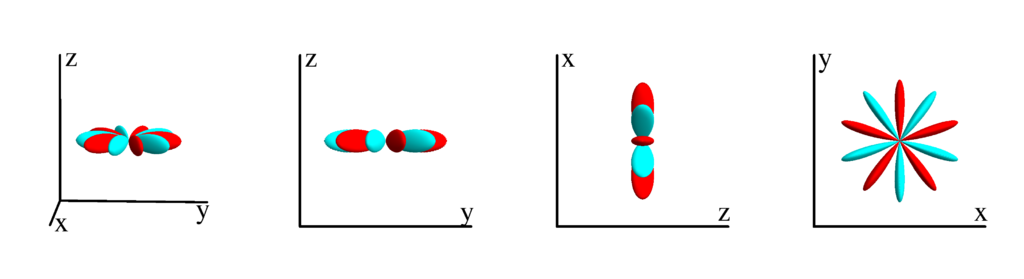
$m_l=-4$
$$ Z_{5}^{(-4)}=\frac{3}{16} \sqrt{\frac{385}{\pi }} \sin ^4(\theta ) \cos (\theta ) \sin (4 \phi )\\ \phantom{Z_{5}^{(-4)}}=\frac{3}{4} \sqrt{\frac{385}{\pi }} x y z (x-y) (x+y) $$
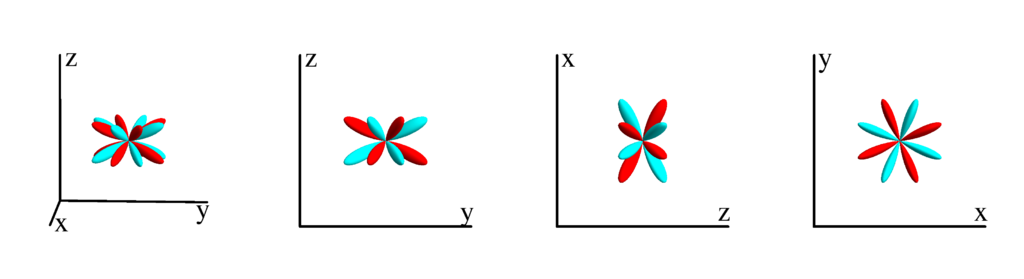
$m_l=-3$
$$ Z_{5}^{(-3)}=\frac{1}{32} \sqrt{\frac{385}{2 \pi }} \sin ^3(\theta ) (9 \cos (2 \theta )+7) \sin (3 \phi )\\ \phantom{Z_{5}^{(-3)}}=\frac{1}{16} \sqrt{\frac{385}{2 \pi }} y \left(y^2-3 x^2\right) \left(x^2+y^2-8 z^2\right) $$
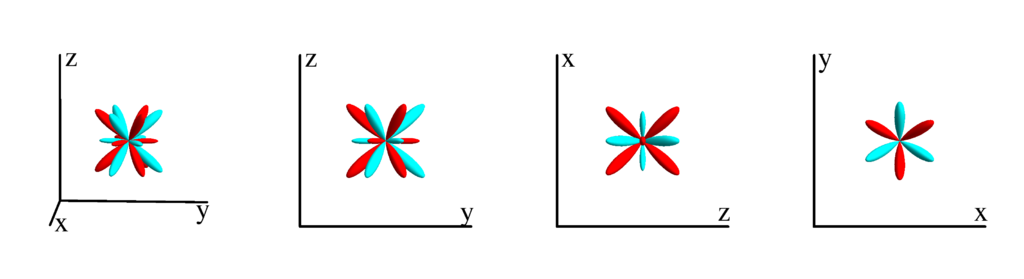
$m_l=-2$
$$ Z_{5}^{(-2)}=\frac{1}{16} \sqrt{\frac{1155}{\pi }} \sin ^2(\theta ) \cos (\theta ) (3 \cos (2 \theta )+1) \sin (2 \phi )\\ \phantom{Z_{5}^{(-2)}}=-\frac{1}{4} \sqrt{\frac{1155}{\pi }} x y z \left(x^2+y^2-2 z^2\right) $$
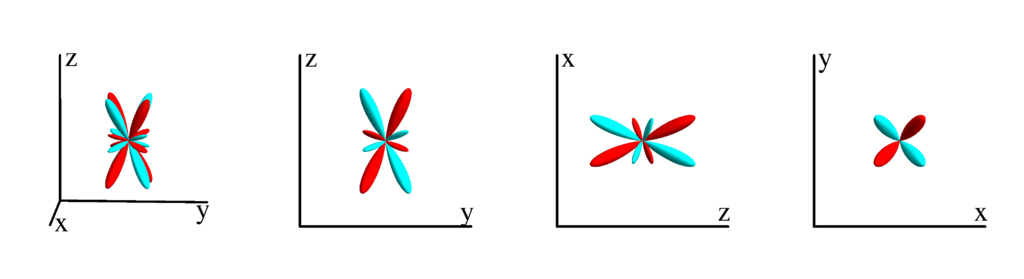
$m_l=-1$
$$ Z_{5}^{(-1)}=\frac{1}{256} \sqrt{\frac{165}{\pi }} (2 \sin (\theta )+7 (\sin (3 \theta )+3 \sin (5 \theta ))) \sin (\phi )\\ \phantom{Z_{5}^{(-1)}}=\frac{1}{16} \sqrt{\frac{165}{\pi }} y \left(-12 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+8 z^4\right) $$
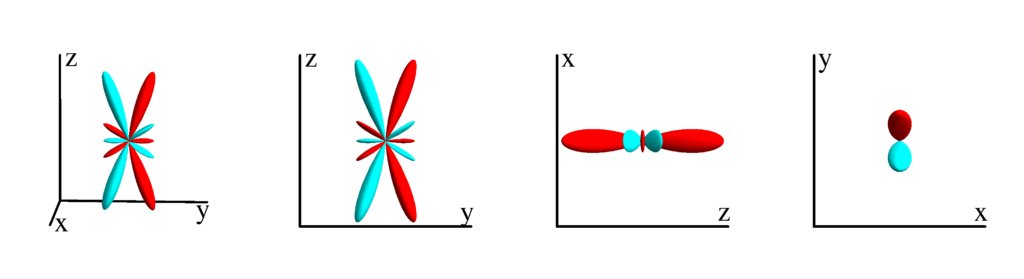
$m_l=0$
$$ Z_{5}^{(0)}=\frac{1}{256} \sqrt{\frac{11}{\pi }} (30 \cos (\theta )+35 \cos (3 \theta )+63 \cos (5 \theta ))\\ \phantom{Z_{5}^{(0)}}=\frac{1}{16} \sqrt{\frac{11}{\pi }} z \left(-40 z^2 \left(x^2+y^2\right)+15 \left(x^2+y^2\right)^2+8 z^4\right) $$

$m_l=1$
$$ Z_{5}^{(1)}=\frac{1}{256} \sqrt{\frac{165}{\pi }} (2 \sin (\theta )+7 (\sin (3 \theta )+3 \sin (5 \theta ))) \cos (\phi )\\ \phantom{Z_{5}^{(1)}}=\frac{1}{16} \sqrt{\frac{165}{\pi }} x \left(-12 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+8 z^4\right) $$
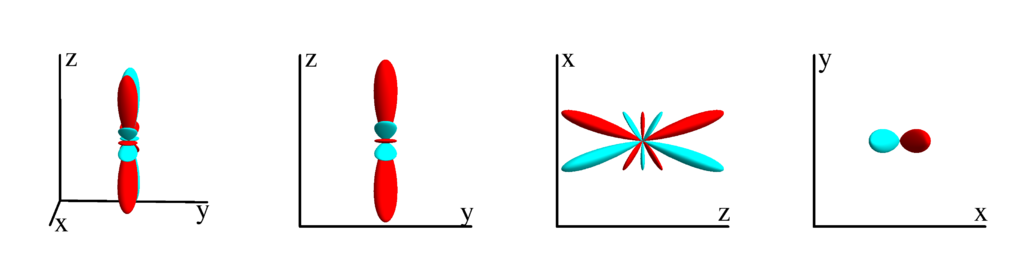
$m_l=2$
$$ Z_{5}^{(2)}=\frac{1}{16} \sqrt{\frac{1155}{\pi }} \sin ^2(\theta ) \cos (\theta ) (3 \cos (2 \theta )+1) \cos (2 \phi )\\ \phantom{Z_{5}^{(2)}}=-\frac{1}{8} \sqrt{\frac{1155}{\pi }} z (x-y) (x+y) \left(x^2+y^2-2 z^2\right) $$
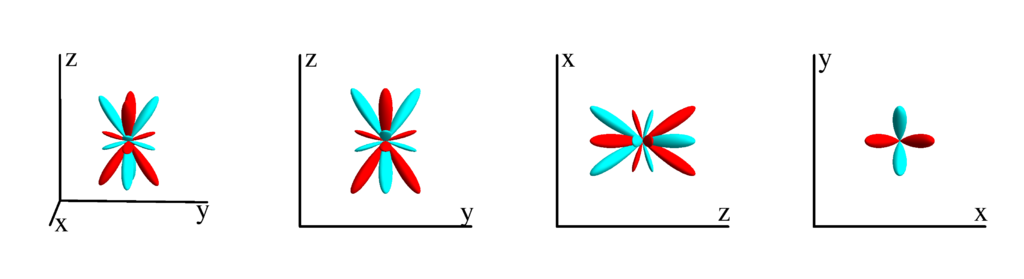
$m_l=3$
$$ Z_{5}^{(3)}=\frac{1}{32} \sqrt{\frac{385}{2 \pi }} \sin ^3(\theta ) (9 \cos (2 \theta )+7) \cos (3 \phi )\\ \phantom{Z_{5}^{(3)}}=-\frac{1}{16} \sqrt{\frac{385}{2 \pi }} x \left(x^2-3 y^2\right) \left(x^2+y^2-8 z^2\right) $$
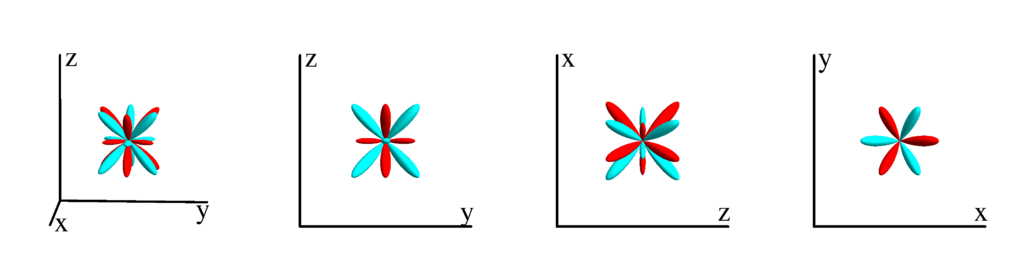
$m_l=4$
$$ Z_{5}^{(4)}=\frac{3}{16} \sqrt{\frac{385}{\pi }} \sin ^4(\theta ) \cos (\theta ) \cos (4 \phi )\\ \phantom{Z_{5}^{(4)}}=\frac{3}{16} \sqrt{\frac{385}{\pi }} z \left(x^4-6 x^2 y^2+y^4\right) $$
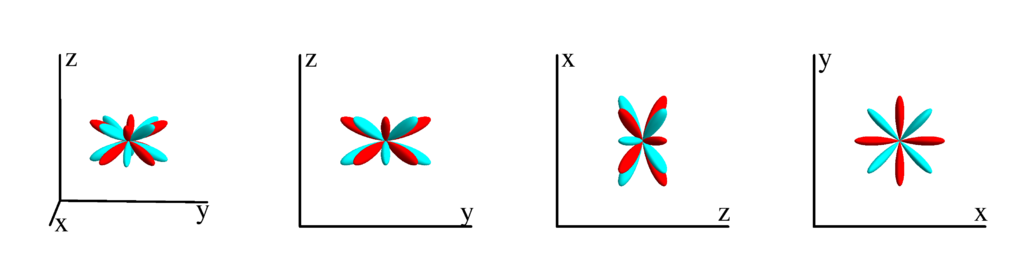
$m_l=5$
$$ Z_{5}^{(5)}=\frac{3}{16} \sqrt{\frac{77}{2 \pi }} \sin ^5(\theta ) \cos (5 \phi )\\ \phantom{Z_{5}^{(5)}}=\frac{3}{16} \sqrt{\frac{77}{2 \pi }} x \left(x^4-10 x^2 y^2+5 y^4\right) $$
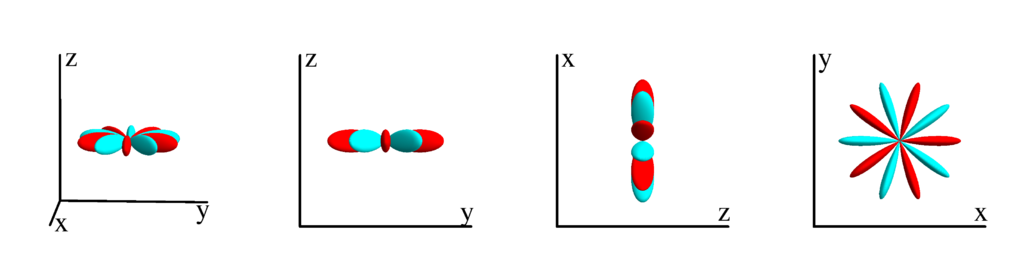
$l=6$
$m_l=-6$
$$ Z_{6}^{(-6)}=\frac{1}{32} \sqrt{\frac{3003}{2 \pi }} \sin ^6(\theta ) \sin (6 \phi )\\ \phantom{Z_{6}^{(-6)}}=\frac{1}{16} \sqrt{\frac{3003}{2 \pi }} x y \left(3 x^4-10 x^2 y^2+3 y^4\right) $$
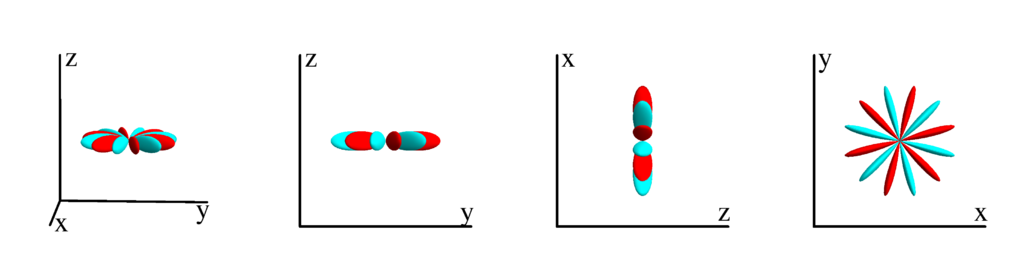
$m_l=-5$
$$ Z_{6}^{(-5)}=\frac{3}{16} \sqrt{\frac{1001}{2 \pi }} \sin ^5(\theta ) \cos (\theta ) \sin (5 \phi )\\ \phantom{Z_{6}^{(-5)}}=\frac{3}{16} \sqrt{\frac{1001}{2 \pi }} y z \left(5 x^4-10 x^2 y^2+y^4\right) $$
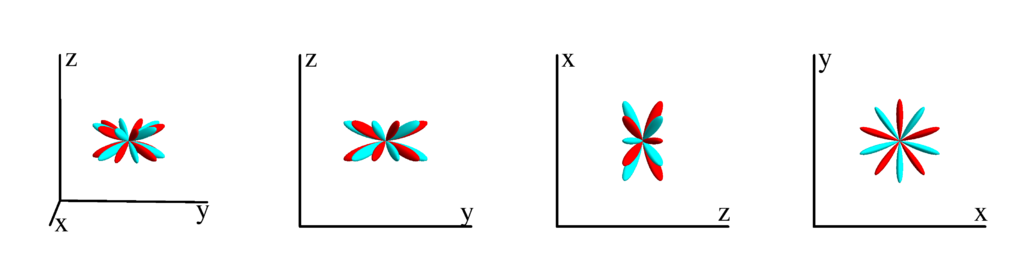
$m_l=-4$
$$ Z_{6}^{(-4)}=\frac{3}{64} \sqrt{\frac{91}{\pi }} \sin ^4(\theta ) (11 \cos (2 \theta )+9) \sin (4 \phi )\\ \phantom{Z_{6}^{(-4)}}=-\frac{3}{8} \sqrt{\frac{91}{\pi }} x y (x-y) (x+y) \left(x^2+y^2-10 z^2\right) $$
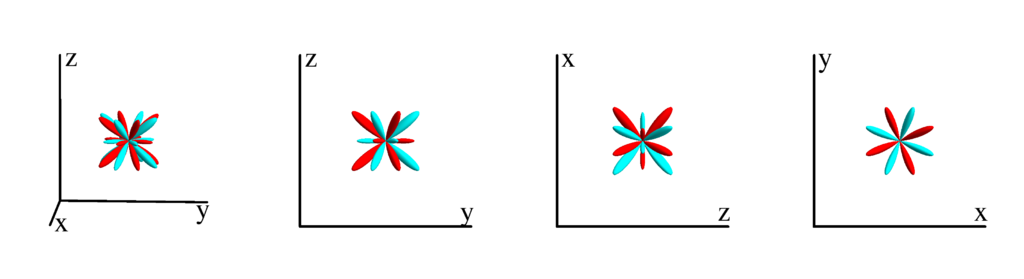
$m_l=-3$
$$ Z_{6}^{(-3)}=\frac{1}{64} \sqrt{\frac{1365}{2 \pi }} \sin ^3(\theta ) (21 \cos (\theta )+11 \cos (3 \theta )) \sin (3 \phi )\\ \phantom{Z_{6}^{(-3)}}=\frac{1}{16} \sqrt{\frac{1365}{2 \pi }} y z \left(y^2-3 x^2\right) \left(3 \left(x^2+y^2\right)-8 z^2\right) $$
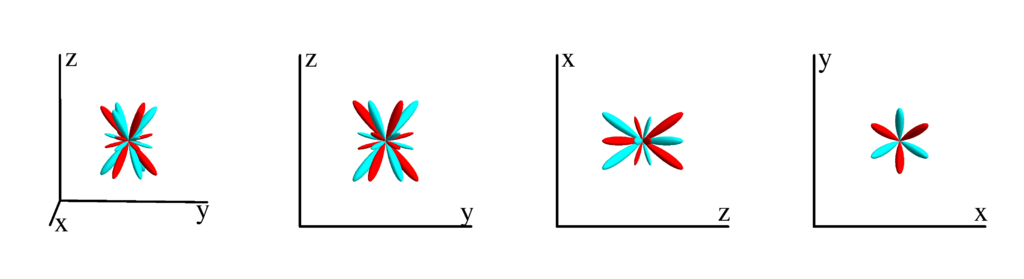
$m_l=-2$
$$ Z_{6}^{(-2)}=\frac{1}{256} \sqrt{\frac{1365}{2 \pi }} \sin ^2(\theta ) (60 \cos (2 \theta )+33 \cos (4 \theta )+35) \sin (2 \phi )\\ \phantom{Z_{6}^{(-2)}}=\frac{1}{16} \sqrt{\frac{1365}{2 \pi }} x y \left(-16 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+16 z^4\right) $$
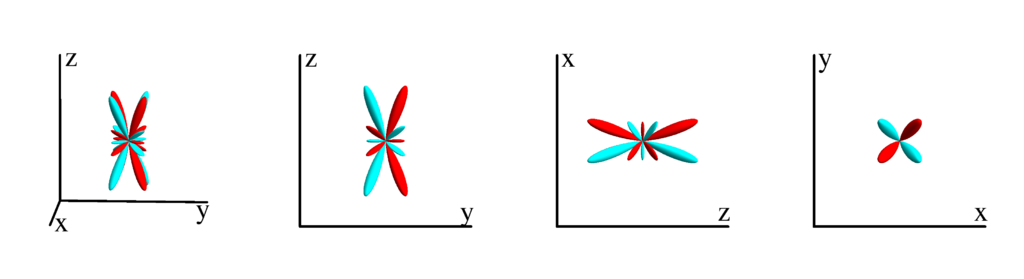
$m_l=-1$
$$ Z_{6}^{(-1)}=\frac{1}{512} \sqrt{\frac{273}{\pi }} (5 \sin (2 \theta )+12 \sin (4 \theta )+33 \sin (6 \theta )) \sin (\phi )\\ \phantom{Z_{6}^{(-1)}}=\frac{1}{16} \sqrt{\frac{273}{\pi }} y z \left(-20 z^2 \left(x^2+y^2\right)+5 \left(x^2+y^2\right)^2+8 z^4\right) $$
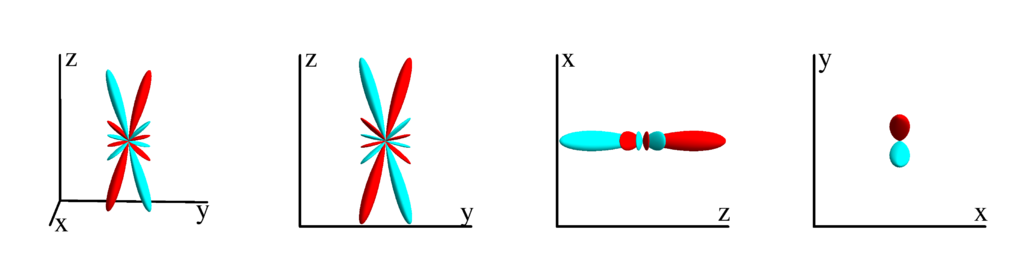
$m_l=0$
$$ Z_{6}^{(0)}=\frac{1}{32} \sqrt{\frac{13}{\pi }} \left(21 \cos ^2(\theta ) \left(11 \cos ^4(\theta )-15 \cos ^2(\theta )+5\right)-5\right)\\ \phantom{Z_{6}^{(0)}}=\frac{1}{32} \sqrt{\frac{13}{\pi }} \left(-120 z^4 \left(x^2+y^2\right)+90 z^2 \left(x^2+y^2\right)^2-5 \left(x^2+y^2\right)^3+16 z^6\right) $$
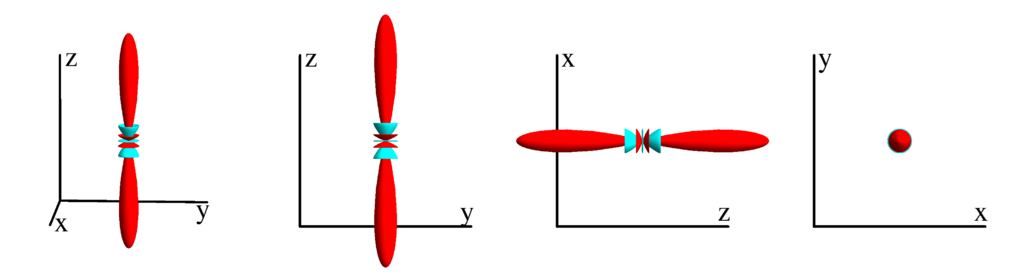
$m_l=1$
$$ Z_{6}^{(1)}=\frac{1}{512} \sqrt{\frac{273}{\pi }} (5 \sin (2 \theta )+12 \sin (4 \theta )+33 \sin (6 \theta )) \cos (\phi )\\ \phantom{Z_{6}^{(1)}}=\frac{1}{16} \sqrt{\frac{273}{\pi }} x z \left(-20 z^2 \left(x^2+y^2\right)+5 \left(x^2+y^2\right)^2+8 z^4\right) $$
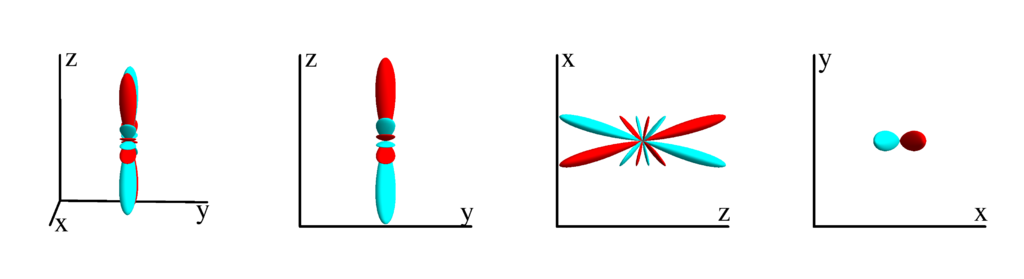
$m_l=2$
$$ Z_{6}^{(2)}=\frac{1}{256} \sqrt{\frac{1365}{2 \pi }} \sin ^2(\theta ) (60 \cos (2 \theta )+33 \cos (4 \theta )+35) \cos (2 \phi )\\ \phantom{Z_{6}^{(2)}}=\frac{1}{32} \sqrt{\frac{1365}{2 \pi }} (x-y) (x+y) \left(-16 z^2 \left(x^2+y^2\right)+\left(x^2+y^2\right)^2+16 z^4\right) $$
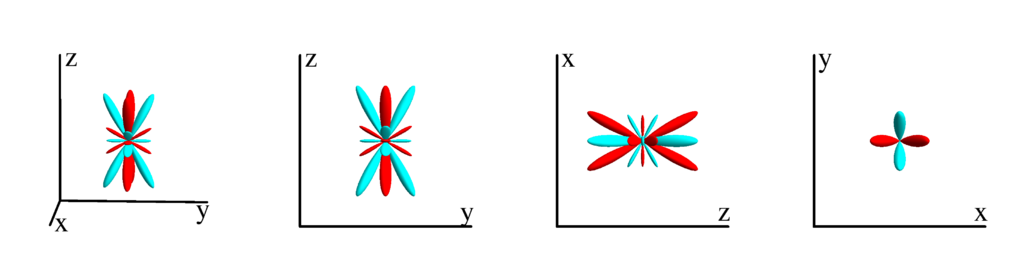
$m_l=3$
$$ Z_{6}^{(3)}=\frac{1}{64} \sqrt{\frac{1365}{2 \pi }} \sin ^3(\theta ) (21 \cos (\theta )+11 \cos (3 \theta )) \cos (3 \phi )\\ \phantom{Z_{6}^{(3)}}=-\frac{1}{16} \sqrt{\frac{1365}{2 \pi }} x z \left(x^2-3 y^2\right) \left(3 \left(x^2+y^2\right)-8 z^2\right) $$
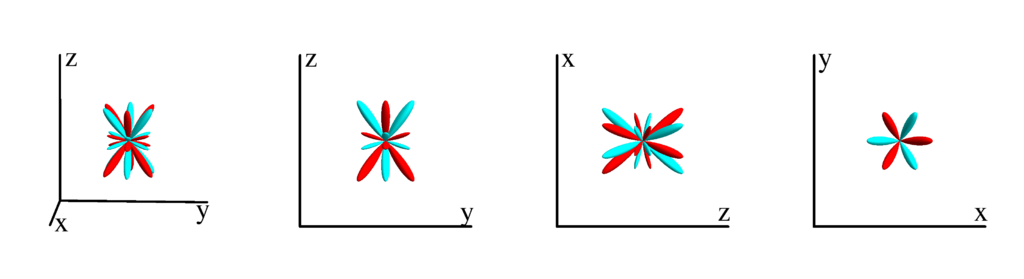
$m_l=4$
$$ Z_{6}^{(4)}=\frac{3}{64} \sqrt{\frac{91}{\pi }} \sin ^4(\theta ) (11 \cos (2 \theta )+9) \cos (4 \phi )\\ \phantom{Z_{6}^{(4)}}=-\frac{3}{32} \sqrt{\frac{91}{\pi }} \left(x^4-6 x^2 y^2+y^4\right) \left(x^2+y^2-10 z^2\right) $$
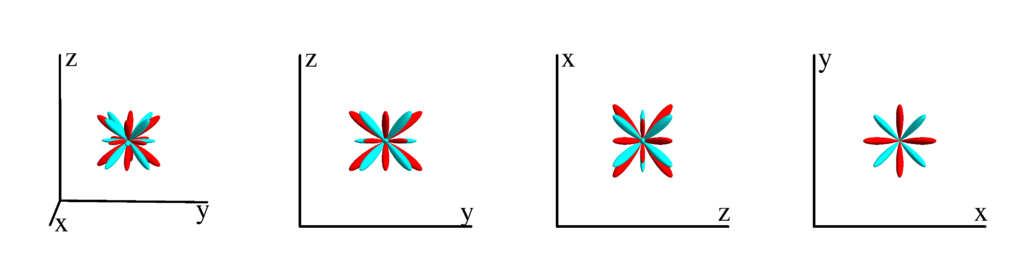
$m_l=5$
$$ Z_{6}^{(5)}=\frac{3}{16} \sqrt{\frac{1001}{2 \pi }} \sin ^5(\theta ) \cos (\theta ) \cos (5 \phi )\\ \phantom{Z_{6}^{(5)}}=\frac{3}{16} \sqrt{\frac{1001}{2 \pi }} x z \left(x^4-10 x^2 y^2+5 y^4\right) $$
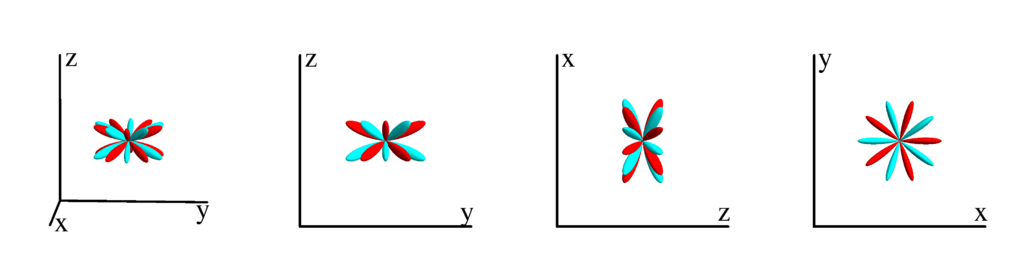
$m_l=6$
$$ Z_{6}^{(6)}=\frac{1}{32} \sqrt{\frac{3003}{2 \pi }} \sin ^6(\theta ) \cos (6 \phi )\\ \phantom{Z_{6}^{(6)}}=\frac{1}{32} \sqrt{\frac{3003}{2 \pi }} \left(x^6-15 x^4 y^2+15 x^2 y^4-y^6\right) $$