Coulomb repulsion $J_H$ and Slater integrals

The Coulomb interaction between two electrons depends on the orbital they are in. The closer the charge density of the two orbitals involved is to each other the larger the Coulomb interaction (given by $\frac{e^2}{|r_1-r_2|}$) between them. For example, for two electrons in the $d$-shell the interaction between an electron in the $d_{x^2-y^2}$ orbital and an electron in the $d_{xy}$ orbital is larger then between an electron in the $d_{z^2}$ orbital and an electron in the $d_{xy}$ orbital.

The Coulomb interaction is given as: $$\begin{equation} H = \sum_{i\neq j} \frac{1}{2} \frac{e^2}{|r_i-r_j|}, \end{equation}$$ whereby the sum runs over all electrons and the factor $1/2$ takes care of the double counting as each pair of electrons only repels once. In second quantization this Hamiltonian can be written as: $$\begin{equation} H = \sum_{\tau_1\tau_2\tau_3\tau_4} U_{\tau_1\tau_2\tau_3\tau_4} a^{\dagger}_{\tau_1}a^{\dagger}_{\tau_2}a^{\phantom{\dagger}}_{\tau_3}a^{\phantom{\dagger}}_{\tau_4}, \end{equation}$$ whereby $\tau$ labels the spin and orbital degrees of freedom.

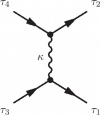Using Feynman diagrams this interaction can be depicted as two electrons entering with quantum numbers $\tau_4$ and $\tau_3$, exchanging an entity $\kappa$ and leaving with quantum numbers $\tau_1$ and $\tau_2$.

Calculating the Coulomb interaction is more difficult as one might expect. The interaction strength diverges when $r_1 = r_2$ and one needs to calculate the principle integral in three dimensions. A good way to evaluate this integral is to expand $1/|r_1-r_2|$ in spherical harmonics and separate the integrals over the angle for the integral over $r$. The angular integrals turn trivial with analytical solutions whereas the radial integral becomes non-divergent. If we assume spherical symmetry for the basis functions the result for the radial integrals are the Slater integrals. If the basis functions are more complex we still can expand these in spherical symmetry and the result is a sum over Slater integrals. The standard operator in Quanty implements the spherical case, the more general case can be created by importing results from DFT and will be discussed in those sections.

The expansion of $e^2/|r_1-r_2|$ is: $$\begin{equation} \sum_{i\neq j} \frac{1}{2} \frac{e^2}{|r_i-r_j|} = \sum_{i\neq j} \frac{1}{2}\sum_{k=0}^{\infty} \sum_{m=-k}^{m=k} \frac{4 \pi e^2}{2k+1} \frac{\mathrm{Min}[r_i,r_j]^k}{\mathrm{Max}[r_i,r_j]^{k+1}} Y_m^{(k)}(\theta_i,\phi_i)Y_m^{(k)}(\theta_j,\phi_j)^*. \end{equation}$$

Expanding our basis states in spherical harmonics times radial wave functions the quantum number $\tau_i$ labels the set of quantum numbers $n_i,l_i,m_i,\sigma_i$. This allows us to separate the radial from angular part of the equation. Using that: $$\begin{eqnarray} &&\sum_i \sqrt{\frac{4 \pi}{2k+1}} Y_m^{(k)}(\theta_i,\phi_i) = \sum_i C_m^{(k)}(\theta_i,\phi_i) \\ \nonumber &&= \sum_{\tau_1,\tau_3} \delta_{\sigma_1,\sigma_3}\delta_{m,m_1-m_3} \left\langle Y_{m_1}^{(l_1)}(\theta,\phi) \left | C_m^{(k)}(\theta,\phi) \right | Y_{m_3}^{(l_3)}(\theta,\phi) \right\rangle a^{\dagger}_{\tau_1}a^{\phantom{\dagger}}_{\tau_3}, \end{eqnarray}$$ we can rewrite: $$\begin{equation} \sum_{i\neq j} \frac{1}{2}\sum_{k=0}^{\infty} \sum_{m=-k}^{m=k} \frac{4 \pi}{2k+1} Y_m^{(k)}(\theta_i,\phi_i)Y_m^{(k)}(\theta_j,\phi_j)^* \end{equation}$$ as: $$\begin{eqnarray} && \frac{1}{2}\sum_{k=0}^{k=\infty}\sum_{\tau_1,\tau_2,\tau_3,\tau_4} \delta_{\sigma_1,\sigma_3}\delta_{\sigma_2,\sigma_4}\delta_{m_4-m_2,m_1-m_3} \times \\ \nonumber && \left\langle Y_{m_1}^{(l_1)} \left | C_{m_1-m_3}^{(k)} \right | Y_{m_3}^{(l_3)} \right\rangle \left\langle Y_{m_4}^{(l_4)} \left | C_{m_4-m_2}^{(k)} \right | Y_{m_2}^{(l_2)} \right\rangle a^{\dagger}_{\tau_1}a^{\phantom{\dagger}}_{\tau_3} a^{\dagger}_{\tau_2}a^{\phantom{\dagger}}_{\tau_4}, \end{eqnarray}$$ which after reordering to normal order becomes: $$\begin{eqnarray} && -\frac{1}{2}\sum_{k=0}^{k=\infty}\sum_{\tau_1,\tau_2,\tau_3,\tau_4} \delta_{\sigma_1,\sigma_3}\delta_{\sigma_2,\sigma_4}\delta_{m_4-m_2,m_1-m_3} \times \\ \nonumber && \left\langle Y_{m_1}^{(l_1)} \left | C_{m_1-m_3}^{(k)} \right | Y_{m_3}^{(l_3)} \right\rangle \left\langle Y_{m_4}^{(l_4)} \left | C_{m_4-m_2}^{(k)} \right | Y_{m_2}^{(l_2)} \right\rangle a^{\dagger}_{\tau_1}a^{\dagger}_{\tau_2}a^{\phantom{\dagger}}_{\tau_3} a^{\phantom{\dagger}}_{\tau_4}. \end{eqnarray}$$

The radial part of the operator ($\frac{\mathrm{Min}[r_i,r_j]^k}{\mathrm{Max}[r_i,r_j]^{k+1}}$) is more difficult and will be cast into parameters: $$\begin{equation} R^{(k)}[\tau_1\tau_2\tau_3\tau_4]=e^2\int_0^{\infty}\int_0^{\infty}\frac{\mathrm{Min}[r_i,r_j]^k}{\mathrm{Max}[r_i,r_j]^{k+1}}R_1[r_i]R_2[r_j]R_3[r_i]R_4[r_j]r_i^2 r_j^2\mathrm{d}r_i\mathrm{d}r_j. \end{equation}$$

Which gives the final result: $$\begin{eqnarray} H &=& \sum_{\tau_1\tau_2\tau_3\tau_4} U_{\tau_1\tau_2\tau_3\tau_4} a^{\dagger}_{\tau_1}a^{\dagger}_{\tau_2}a^{\phantom{\dagger}}_{\tau_3}a^{\phantom{\dagger}}_{\tau_4},\\ \nonumber U_{\tau_1\tau_2\tau_3\tau_4} &=& -\frac{1}{2}\delta_{\sigma_1,\sigma_3}\delta_{\sigma_2,\sigma_4} \sum_{k=0}^{\infty}c^{(k)}[l_1,m_1;l_3,m_3]c^{(k)}[l_4,m_4;l_2,m_2]\\ \nonumber &&\quad \times R^{(k)}[\tau_1\tau_2\tau_3\tau_4],\\ \nonumber c^{(k)}[l_1,m_1;l_2,m_2] &=& \left\langle Y_{m_1}^{(l_1)} \left | C_{m_1-m_2}^{(k)} \right | Y_{m_2}^{(l_2)} \right\rangle. \end{eqnarray}$$

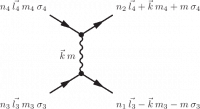Using angular momentum as a basis the scattering event described is given by the diagram on the left. An angular momentum $\vec{k}$ with a projection $m$ on the $z$ direction is exchanged.

Using conservation of angular momentum we can see that $|l_1-l_3| \leq k \leq |l_1+l_3|$ and $|l_2-l_4| \leq k \leq |l_2+l_4|$. This can be used to restrict the number of radial integrals one needs to compute.