XAS $L_{2,3}$ as conductivity tensor
Absorption spectra are polarization dependent. In principle one can choose an infinite different number of polarizations. Calculating for each different experimental geometry (or polarization) a new spectrum is cumbersome and not needed. The material properties are given by the conductivity tensor. For dipole transitions a 3 by 3 matrix. The absorption spectra for a given experiment are then found by the relation: \begin{equation} I(\omega,\epsilon) = -\mathrm{Im}[\epsilon^* \cdot \sigma(\omega) \cdot \epsilon], \end{equation} with $\epsilon$ the polarization vector, $\omega$ the photon energy, $\sigma(\omega)$ the energy dependent conductivity tensor, and $I$ the measured intensity. Quanty can calculate the conductivity tensor. This is an extra option given to the function CreateSpectra (\{“Tensor”,true\}).
The example below calculates the conductivity tensor at the Ni $L_{2,3}$ edge. We show two different methods. The first calculates 9 spectra and by linear combining them retrieves the tensor. Method two uses a Block algorithm.
- XAS_tensor.Quanty
-- here we calculate the 2p to 3d x-ray absorption of NiO within the Ligand-field theory -- approximation. The first part of the script is very much the same as calculating -- the ground-state with the addition that we now also need a 2p core shell in the basis -- from the previous example we know that within NiO there are 3 states close to each other -- and then there is an energy gap of about 1 eV. We thus only need to consider the 3 -- lowest states (Npsi=3 later on) -- the spectra are represented as a 3 by 3 tensor, the conductivity tensor. We show two -- different methods to calculate this tensor, once creating 9 spectra with different -- polarizations, once using the option Tensor in the CreateSpectra function NF=26 NB=0 IndexDn_2p={ 0, 2, 4} IndexUp_2p={ 1, 3, 5} IndexDn_3d={ 6, 8,10,12,14} IndexUp_3d={ 7, 9,11,13,15} IndexDn_Ld={16,18,20,22,24} IndexUp_Ld={17,19,21,23,25} -- angular momentum operators on the d-shell OppSx_3d =NewOperator("Sx" ,NF, IndexUp_3d, IndexDn_3d) OppSy_3d =NewOperator("Sy" ,NF, IndexUp_3d, IndexDn_3d) OppSz_3d =NewOperator("Sz" ,NF, IndexUp_3d, IndexDn_3d) OppSsqr_3d =NewOperator("Ssqr" ,NF, IndexUp_3d, IndexDn_3d) OppSplus_3d=NewOperator("Splus",NF, IndexUp_3d, IndexDn_3d) OppSmin_3d =NewOperator("Smin" ,NF, IndexUp_3d, IndexDn_3d) OppLx_3d =NewOperator("Lx" ,NF, IndexUp_3d, IndexDn_3d) OppLy_3d =NewOperator("Ly" ,NF, IndexUp_3d, IndexDn_3d) OppLz_3d =NewOperator("Lz" ,NF, IndexUp_3d, IndexDn_3d) OppLsqr_3d =NewOperator("Lsqr" ,NF, IndexUp_3d, IndexDn_3d) OppLplus_3d=NewOperator("Lplus",NF, IndexUp_3d, IndexDn_3d) OppLmin_3d =NewOperator("Lmin" ,NF, IndexUp_3d, IndexDn_3d) OppJx_3d =NewOperator("Jx" ,NF, IndexUp_3d, IndexDn_3d) OppJy_3d =NewOperator("Jy" ,NF, IndexUp_3d, IndexDn_3d) OppJz_3d =NewOperator("Jz" ,NF, IndexUp_3d, IndexDn_3d) OppJsqr_3d =NewOperator("Jsqr" ,NF, IndexUp_3d, IndexDn_3d) OppJplus_3d=NewOperator("Jplus",NF, IndexUp_3d, IndexDn_3d) OppJmin_3d =NewOperator("Jmin" ,NF, IndexUp_3d, IndexDn_3d) Oppldots_3d=NewOperator("ldots",NF, IndexUp_3d, IndexDn_3d) -- Angular momentum operators on the Ligand shell OppSx_Ld =NewOperator("Sx" ,NF, IndexUp_Ld, IndexDn_Ld) OppSy_Ld =NewOperator("Sy" ,NF, IndexUp_Ld, IndexDn_Ld) OppSz_Ld =NewOperator("Sz" ,NF, IndexUp_Ld, IndexDn_Ld) OppSsqr_Ld =NewOperator("Ssqr" ,NF, IndexUp_Ld, IndexDn_Ld) OppSplus_Ld=NewOperator("Splus",NF, IndexUp_Ld, IndexDn_Ld) OppSmin_Ld =NewOperator("Smin" ,NF, IndexUp_Ld, IndexDn_Ld) OppLx_Ld =NewOperator("Lx" ,NF, IndexUp_Ld, IndexDn_Ld) OppLy_Ld =NewOperator("Ly" ,NF, IndexUp_Ld, IndexDn_Ld) OppLz_Ld =NewOperator("Lz" ,NF, IndexUp_Ld, IndexDn_Ld) OppLsqr_Ld =NewOperator("Lsqr" ,NF, IndexUp_Ld, IndexDn_Ld) OppLplus_Ld=NewOperator("Lplus",NF, IndexUp_Ld, IndexDn_Ld) OppLmin_Ld =NewOperator("Lmin" ,NF, IndexUp_Ld, IndexDn_Ld) OppJx_Ld =NewOperator("Jx" ,NF, IndexUp_Ld, IndexDn_Ld) OppJy_Ld =NewOperator("Jy" ,NF, IndexUp_Ld, IndexDn_Ld) OppJz_Ld =NewOperator("Jz" ,NF, IndexUp_Ld, IndexDn_Ld) OppJsqr_Ld =NewOperator("Jsqr" ,NF, IndexUp_Ld, IndexDn_Ld) OppJplus_Ld=NewOperator("Jplus",NF, IndexUp_Ld, IndexDn_Ld) OppJmin_Ld =NewOperator("Jmin" ,NF, IndexUp_Ld, IndexDn_Ld) -- total angular momentum OppSx = OppSx_3d + OppSx_Ld OppSy = OppSy_3d + OppSy_Ld OppSz = OppSz_3d + OppSz_Ld OppSsqr = OppSx * OppSx + OppSy * OppSy + OppSz * OppSz OppLx = OppLx_3d + OppLx_Ld OppLy = OppLy_3d + OppLy_Ld OppLz = OppLz_3d + OppLz_Ld OppLsqr = OppLx * OppLx + OppLy * OppLy + OppLz * OppLz OppJx = OppJx_3d + OppJx_Ld OppJy = OppJy_3d + OppJy_Ld OppJz = OppJz_3d + OppJz_Ld OppJsqr = OppJx * OppJx + OppJy * OppJy + OppJz * OppJz -- define the coulomb operator -- we here define the part depending on F0 seperately from the part depending on F2 -- when summing we can put in the numerical values of the slater integrals OppF0_3d =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2_3d =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4_3d =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,0,1}) -- define onsite energies - crystal field -- Akm = {{k1,m1,Akm1},{k2,m2,Akm2}, ... } Akm = PotentialExpandedOnClm("Oh", 2, {0.6,-0.4}) OpptenDq_3d = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) OpptenDq_Ld = NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, Akm) Akm = PotentialExpandedOnClm("Oh", 2, {1,0}) OppNeg_3d = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) OppNeg_Ld = NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, Akm) Akm = PotentialExpandedOnClm("Oh", 2, {0,1}) OppNt2g_3d = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) OppNt2g_Ld = NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, Akm) OppNUp_2p = NewOperator("Number", NF, IndexUp_2p, IndexUp_2p, {1,1,1}) OppNDn_2p = NewOperator("Number", NF, IndexDn_2p, IndexDn_2p, {1,1,1}) OppN_2p = OppNUp_2p + OppNDn_2p OppNUp_3d = NewOperator("Number", NF, IndexUp_3d, IndexUp_3d, {1,1,1,1,1}) OppNDn_3d = NewOperator("Number", NF, IndexDn_3d, IndexDn_3d, {1,1,1,1,1}) OppN_3d = OppNUp_3d + OppNDn_3d OppNUp_Ld = NewOperator("Number", NF, IndexUp_Ld, IndexUp_Ld, {1,1,1,1,1}) OppNDn_Ld = NewOperator("Number", NF, IndexDn_Ld, IndexDn_Ld, {1,1,1,1,1}) OppN_Ld = OppNUp_Ld + OppNDn_Ld -- define L-d interaction Akm = PotentialExpandedOnClm("Oh", 2, {1,0}) OppVeg = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_Ld, IndexDn_Ld,Akm) + NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh", 2, {0,1}) OppVt2g = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_Ld, IndexDn_Ld,Akm) + NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, IndexUp_3d, IndexDn_3d, Akm) -- core valence interaction Oppcldots= NewOperator("ldots", NF, IndexUp_2p, IndexDn_2p) OppUpdF0 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {1,0}, {0,0}) OppUpdF2 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,1}, {0,0}) OppUpdG1 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {1,0}) OppUpdG3 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {0,1}) -- dipole transition t=math.sqrt(1/2) Akm = {{1,-1,t},{1, 1,-t}} TXASx = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) Akm = {{1,-1,t*I},{1, 1,t*I}} TXASy = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) Akm = {{1,0,1}} TXASz = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) TXASr = t*(TXASx - I * TXASy) TXASl =-t*(TXASx + I * TXASy) -- We follow the energy definitions as introduced in the group of G.A. Sawatzky (Groningen) -- J. Zaanen, G.A. Sawatzky, and J.W. Allen PRL 55, 418 (1985) -- for parameters of specific materials see -- A.E. Bockquet et al. PRB 55, 1161 (1996) -- After some initial discussion the energies U and Delta refer to the center of a configuration -- The L^10 d^n configuration has an energy 0 -- The L^9 d^n+1 configuration has an energy Delta -- The L^8 d^n+2 configuration has an energy 2*Delta+Udd -- -- If we relate this to the onsite energy of the L and d orbitals we find -- 10 eL + n ed + n(n-1) U/2 == 0 -- 9 eL + (n+1) ed + (n+1)n U/2 == Delta -- 8 eL + (n+2) ed + (n+1)(n+2) U/2 == 2*Delta+U -- 3 equations with 2 unknowns, but with interdependence yield: -- ed = (10*Delta-nd*(19+nd)*U/2)/(10+nd) -- eL = nd*((1+nd)*Udd/2-Delta)/(10+nd) -- -- For the final state we/they defined -- The 2p^5 L^10 d^n+1 configuration has an energy 0 -- The 2p^5 L^9 d^n+2 configuration has an energy Delta + Udd - Upd -- The 2p^5 L^8 d^n+3 configuration has an energy 2*Delta + 3*Udd - 2*Upd -- -- If we relate this to the onsite energy of the p and d orbitals we find -- 6 ep + 10 eL + n ed + n(n-1) Udd/2 + 6 n Upd == 0 -- 6 ep + 9 eL + (n+1) ed + (n+1)n Udd/2 + 6 (n+1) Upd == Delta -- 6 ep + 8 eL + (n+2) ed + (n+1)(n+2) Udd/2 + 6 (n+2) Upd == 2*Delta+Udd -- 5 ep + 10 eL + (n+1) ed + (n+1)(n) Udd/2 + 5 (n+1) Upd == 0 -- 5 ep + 9 eL + (n+2) ed + (n+2)(n+1) Udd/2 + 5 (n+2) Upd == Delta+Udd-Upd -- 5 ep + 8 eL + (n+3) ed + (n+3)(n+2) Udd/2 + 5 (n+3) Upd == 2*Delta+3*Udd-2*Upd -- 6 equations with 3 unknowns, but with interdependence yield: -- epfinal = (10*Delta + (1+nd)*(nd*Udd/2-(10+nd)*Upd) / (16+nd) -- edfinal = (10*Delta - nd*(31+nd)*Udd/2-90*Upd) / (16+nd) -- eLfinal = ((1+nd)*(nd*Udd/2+6*Upd)-(6+nd)*Delta) / (16+nd) -- -- -- -- note that ed-ep = Delta - nd * U and not Delta -- note furthermore that ep and ed here are defined for the onsite energy if the system had -- locally nd electrons in the d-shell. In DFT or Hartree Fock the d occupation is in the end not -- nd and thus the onsite energy of the Kohn-Sham orbitals is not equal to ep and ed in model -- calculations. -- -- note furthermore that ep and eL actually should be different for most systems. We happily ignore this fact -- -- We normally take U and Delta as experimentally determined parameters -- number of electrons (formal valence) nd = 8 -- parameters from experiment (core level PES) Udd = 7.3 Upd = 8.5 Delta = 4.7 -- parameters obtained from DFT (PRB 85, 165113 (2012)) F2dd = 11.14 F4dd = 6.87 F2pd = 6.67 G1pd = 4.92 G3pd = 2.80 tenDq = 0.56 tenDqL = 1.44 Veg = 2.06 Vt2g = 1.21 zeta_3d = 0.081 zeta_2p = 11.51 Bz = 0.000001 Hz = 0.120 ed = (10*Delta-nd*(19+nd)*Udd/2)/(10+nd) eL = nd*((1+nd)*Udd/2-Delta)/(10+nd) epfinal = (10*Delta + (1+nd)*(nd*Udd/2-(10+nd)*Upd)) / (16+nd) edfinal = (10*Delta - nd*(31+nd)*Udd/2-90*Upd) / (16+nd) eLfinal = ((1+nd)*(nd*Udd/2+6*Upd) - (6+nd)*Delta) / (16+nd) F0dd = Udd + (F2dd+F4dd) * 2/63 F0pd = Upd + (1/15)*G1pd + (3/70)*G3pd Hamiltonian = F0dd*OppF0_3d + F2dd*OppF2_3d + F4dd*OppF4_3d + zeta_3d*Oppldots_3d + Bz*(2*OppSz_3d + OppLz_3d) + Hz * OppSz_3d + tenDq*OpptenDq_3d + tenDqL*OpptenDq_Ld + Veg * OppVeg + Vt2g * OppVt2g + ed * OppN_3d + eL * OppN_Ld XASHamiltonian = F0dd*OppF0_3d + F2dd*OppF2_3d + F4dd*OppF4_3d + zeta_3d*Oppldots_3d + Bz*(2*OppSz_3d + OppLz_3d)+ Hz * OppSz_3d + tenDq*OpptenDq_3d + tenDqL*OpptenDq_Ld + Veg * OppVeg + Vt2g * OppVt2g + edfinal * OppN_3d + eLfinal * OppN_Ld + epfinal * OppN_2p + zeta_2p * Oppcldots + F0pd * OppUpdF0 + F2pd * OppUpdF2 + G1pd * OppUpdG1 + G3pd * OppUpdG3 -- we now can create the lowest Npsi eigenstates: Npsi=3 -- in order to make sure we have a filling of 8 electrons we need to define some restrictions StartRestrictions = {NF, NB, {"000000 1111111111 0000000000",8,8}, {"111111 0000000000 1111111111",16,16}} psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi) oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSz_3d, OppLz_3d, Oppldots_3d, OppF2_3d, OppF4_3d, OppNeg_3d, OppNt2g_3d, OppNeg_Ld, OppNt2g_Ld, OppN_3d} -- print of some expectation values print(" # <E> <S^2> <L^2> <J^2> <S_z^3d> <L_z^3d> <l.s> <F[2]> <F[4]> <Neg^3d> <Nt2g^3d><Neg^Ld> <Nt2g^Ld><N^3d>"); for i = 1,#psiList do io.write(string.format("%3i ",i)) for j = 1,#oppList do expectationvalue = Chop(psiList[i]*oppList[j]*psiList[i]) io.write(string.format("%8.3f ",expectationvalue)) end io.write("\n") end -- calculating the spectra is simple and single line once all operators and wave-functions -- are defined. --------------------------- Method 1 ----------------------------- -- in order to create the tensor we define 9 spectra using operators that are combinations -- of x, y and z polarized light TXASypz = sqrt(1/2)*(TXASy + TXASz) TXASzpx = sqrt(1/2)*(TXASz + TXASx) TXASxpy = sqrt(1/2)*(TXASx + TXASy) TXASypiz = sqrt(1/2)*(TXASy + I * TXASz) TXASzpix = sqrt(1/2)*(TXASz + I * TXASx) TXASxpiy = sqrt(1/2)*(TXASx + I * TXASy) TimeStart("Mehtod1") XASSpectra = CreateSpectra(XASHamiltonian, {TXASx,TXASy,TXASz,TXASypz,TXASzpx,TXASxpy,TXASypiz,TXASzpix,TXASxpiy}, psiList[1], {{"Emin",-10}, {"Emax",20}, {"NE",3000}, {"Gamma",0.1}}) TimeEnd("Mehtod1") -- Broaden these 9 spectra TimeStart("Broaden") XASSpectra.Broaden(0.4, {{-3.7, 0.45}, {-2.2, 0.65}, { 0.0, 0.65}, { 8 , 0.80}, {13.2, 0.80}, {14.0, 1.075}, {16.0, 1.075}}) TimeEnd("Broaden") -- linear combine them into a tensor (note that the order here is given by the list of operators in the CreateSpectra function XASSigma_method1 = Spectra.Sum(XASSpectra,{1,0,0, 0,0,0, 0, 0,0}, {-(1-I)/2,-(1-I)/2,0, 0,0,1, 0,0,-I}, {-(1+I)/2,0,-(1+I)/2, 0,1,0, 0,I,0 } ,{-(1+I)/2,-(1+I)/2,0, 0,0,1, 0, 0,I}, {0,1,0, 0,0,0, 0,0,0}, {0,-(1-I)/2,-(1-I)/2, 1,0,0, -I,0,0} ,{-(1-I)/2,0,-(1-I)/2, 0,1,0, 0,-I,0}, {0,-(1+I)/2,-(1+I)/2, 1,0,0, I,0, 0}, {0,0,1, 0,0,0, 0,0,0}) XASSigma_method1.Print({{"file","XASSigma_method1.dat"}}) -- prepare the gnuplot output for Sigma gnuplotInput = [[ set autoscale # scale axes automatically set xtic auto # set xtics automatically set ytic auto # set ytics automatically set style line 1 lt 1 lw 2 lc 1 set style line 2 lt 1 lw 2 lc 3 set xlabel "E (eV)" font "Times,10" set ylabel "Intensity (arb. units)" font "Times,10" set yrange [-0.3:0.3] set out 'SigmaTensor_method1.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 set multiplot layout 6, 3 plot "XASSigma_method1.dat" u 1:2 title 'Re[{/Symbol s}_{xx}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:3 title 'Im[{/Symbol s}_{xx}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:4 title 'Re[{/Symbol s}_{xy}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:5 title 'Im[{/Symbol s}_{xy}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:6 title 'Re[{/Symbol s}_{xz}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:7 title 'Im[{/Symbol s}_{xz}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:8 title 'Re[{/Symbol s}_{yx}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:9 title 'Im[{/Symbol s}_{yx}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:10 title 'Re[{/Symbol s}_{yy}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:11 title 'Im[{/Symbol s}_{yy}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:12 title 'Re[{/Symbol s}_{yz}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:13 title 'Im[{/Symbol s}_{yz}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:14 title 'Re[{/Symbol s}_{zx}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:15 title 'Im[{/Symbol s}_{zx}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:16 title 'Re[{/Symbol s}_{zy}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:17 title 'Im[{/Symbol s}_{zy}]' with lines ls 2 plot "XASSigma_method1.dat" u 1:18 title 'Re[{/Symbol s}_{zz}]' with lines ls 1,\ "XASSigma_method1.dat" u 1:19 title 'Im[{/Symbol s}_{zz}]' with lines ls 2 unset multiplot ]] print("Prepare gnuplot-file for Sigma") -- write the gnuplot script to a file file = io.open("SigmaTensor_method1.gnuplot", "w") file:write(gnuplotInput) file:close() print("") print("Execute the gnuplot to produce plots and convert the output into a pdf-file") -- call gnuplot to execute the script os.execute("gnuplot SigmaTensor_method1.gnuplot ; ps2pdf SigmaTensor_method1.ps ; ps2eps SigmaTensor_method1.ps ; mv SigmaTensor_method1.eps temp.eps ; eps2eps temp.eps SigmaTensor_method1.eps ; rm temp.eps") --------------------------- Method 2 ----------------------------- TimeStart("Mehtod2") XASSigma_method2, SigmaTri = CreateSpectra(XASHamiltonian, {TXASx,TXASy,TXASz}, psiList[1], {{"Emin",-10}, {"Emax",20}, {"NE",3000}, {"Gamma",0.1}, {"Tensor",true}}) TimeEnd("Mehtod2") -- Broaden these 9 spectra TimeStart("Broaden") XASSigma_method2.Broaden(0.4, {{-3.7, 0.45}, {-2.2, 0.65}, { 0.0, 0.65}, { 8 , 0.80}, {13.2, 0.80}, {14.0, 1.075}, {16.0, 1.075}}) TimeEnd("Broaden") XASSigma_method2.Print({{"file","XASSigma_method2.dat"}}) -- prepare the gnuplot output for Sigma gnuplotInput = [[ set autoscale # scale axes automatically set xtic auto # set xtics automatically set ytic auto # set ytics automatically set style line 1 lt 1 lw 2 lc 1 set style line 2 lt 1 lw 2 lc 3 set xlabel "E (eV)" font "Times,10" set ylabel "Intensity (arb. units)" font "Times,10" set yrange [-0.3:0.3] set out 'SigmaTensor_method2.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 set multiplot layout 6, 3 plot "XASSigma_method2.dat" u 1:2 title 'Re[{/Symbol s}_{xx}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:3 title 'Im[{/Symbol s}_{xx}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:4 title 'Re[{/Symbol s}_{xy}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:5 title 'Im[{/Symbol s}_{xy}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:6 title 'Re[{/Symbol s}_{xz}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:7 title 'Im[{/Symbol s}_{xz}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:8 title 'Re[{/Symbol s}_{yx}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:9 title 'Im[{/Symbol s}_{yx}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:10 title 'Re[{/Symbol s}_{yy}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:11 title 'Im[{/Symbol s}_{yy}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:12 title 'Re[{/Symbol s}_{yz}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:13 title 'Im[{/Symbol s}_{yz}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:14 title 'Re[{/Symbol s}_{zx}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:15 title 'Im[{/Symbol s}_{zx}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:16 title 'Re[{/Symbol s}_{zy}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:17 title 'Im[{/Symbol s}_{zy}]' with lines ls 2 plot "XASSigma_method2.dat" u 1:18 title 'Re[{/Symbol s}_{zz}]' with lines ls 1,\ "XASSigma_method2.dat" u 1:19 title 'Im[{/Symbol s}_{zz}]' with lines ls 2 unset multiplot ]] print("Prepare gnuplot-file for Sigma") -- write the gnuplot script to a file file = io.open("SigmaTensor_method2.gnuplot", "w") file:write(gnuplotInput) file:close() print("") print("Execute the gnuplot to produce plots and convert the output into a pdf-file") -- call gnuplot to execute the script os.execute("gnuplot SigmaTensor_method2.gnuplot ; ps2pdf SigmaTensor_method2.ps ; ps2eps SigmaTensor_method2.ps ; mv SigmaTensor_method2.eps temp.eps ; eps2eps temp.eps SigmaTensor_method2.eps ; rm temp.eps") -------------------------- difference ------------------------ XASSigma_diff = XASSigma_method2 - XASSigma_method1 XASSigma_diff.Print({{"file","XASSigma_diff.dat"}}) -- prepare the gnuplot output for Sigma gnuplotInput = [[ set autoscale # scale axes automatically set xtic auto # set xtics automatically set ytic auto # set ytics automatically set style line 1 lt 1 lw 2 lc 1 set style line 2 lt 1 lw 2 lc 3 set xlabel "E (eV)" font "Times,10" set ylabel "Intensity (arb. units * 1000 000 000)" font "Times,10" set yrange [-0.3:0.3] scale = 1000000000 set out 'XASSigma_diff.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 set multiplot layout 6, 3 plot "XASSigma_diff.dat" u 1:($2*scale) title 'Re[{/Symbol s}_{xx}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($3*scale) title 'Im[{/Symbol s}_{xx}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($4*scale) title 'Re[{/Symbol s}_{xy}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($5*scale) title 'Im[{/Symbol s}_{xy}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($6*scale) title 'Re[{/Symbol s}_{xz}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($7*scale) title 'Im[{/Symbol s}_{xz}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($8*scale) title 'Re[{/Symbol s}_{yx}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($9*scale) title 'Im[{/Symbol s}_{yx}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($10*scale) title 'Re[{/Symbol s}_{yy}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($11*scale) title 'Im[{/Symbol s}_{yy}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($12*scale) title 'Re[{/Symbol s}_{yz}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($13*scale) title 'Im[{/Symbol s}_{yz}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($14*scale) title 'Re[{/Symbol s}_{zx}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($15*scale) title 'Im[{/Symbol s}_{zx}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($16*scale) title 'Re[{/Symbol s}_{zy}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($17*scale) title 'Im[{/Symbol s}_{zy}]' with lines ls 2 plot "XASSigma_diff.dat" u 1:($18*scale) title 'Re[{/Symbol s}_{zz}]' with lines ls 1,\ "XASSigma_diff.dat" u 1:($19*scale) title 'Im[{/Symbol s}_{zz}]' with lines ls 2 unset multiplot ]] print("Prepare gnuplot-file for Sigma") -- write the gnuplot script to a file file = io.open("XASSigma_diff.gnuplot", "w") file:write(gnuplotInput) file:close() print("") print("Execute the gnuplot to produce plots and convert the output into a pdf-file") -- call gnuplot to execute the script os.execute("gnuplot XASSigma_diff.gnuplot ; ps2pdf XASSigma_diff.ps ; ps2eps XASSigma_diff.ps ; mv XASSigma_diff.eps temp.eps ; eps2eps temp.eps XASSigma_diff.eps ; rm temp.eps") ---------------- overview of timing ------------------- TimePrint()
The resulting spectra are for method 1 are:
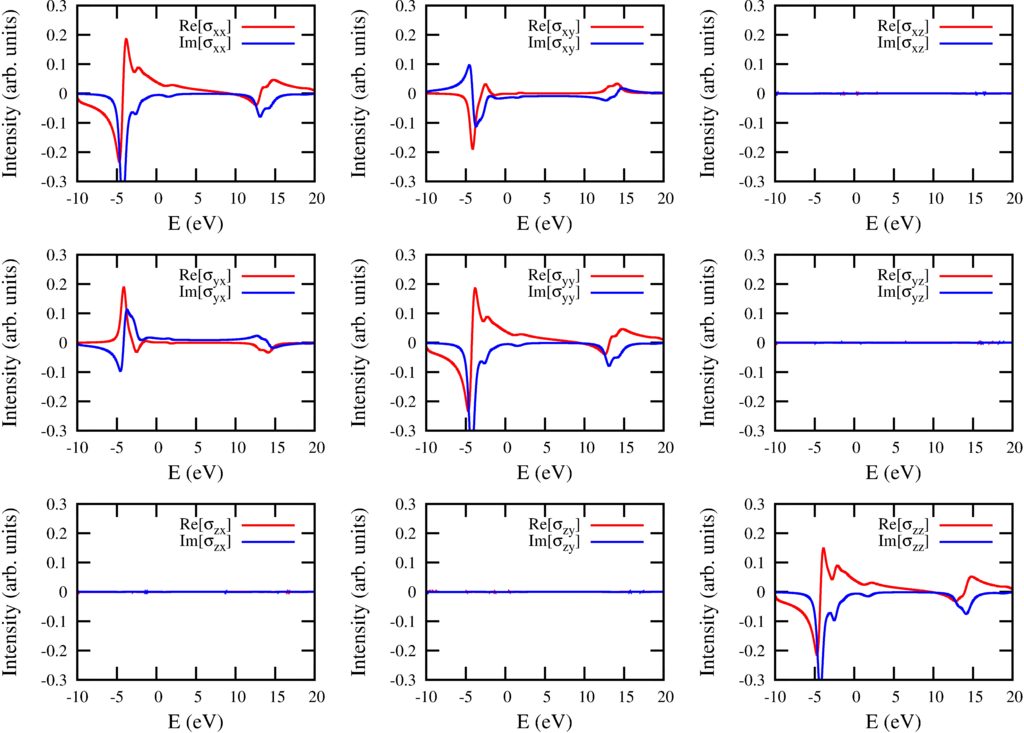 |
| $2p$ to $3d$ excitations for all possible polarizations represented as a conductivity tensor. Calculated using 9 spectra of different rotated polarization and linear combining. |
|---|
###
The resulting spectra are for method 2 are:
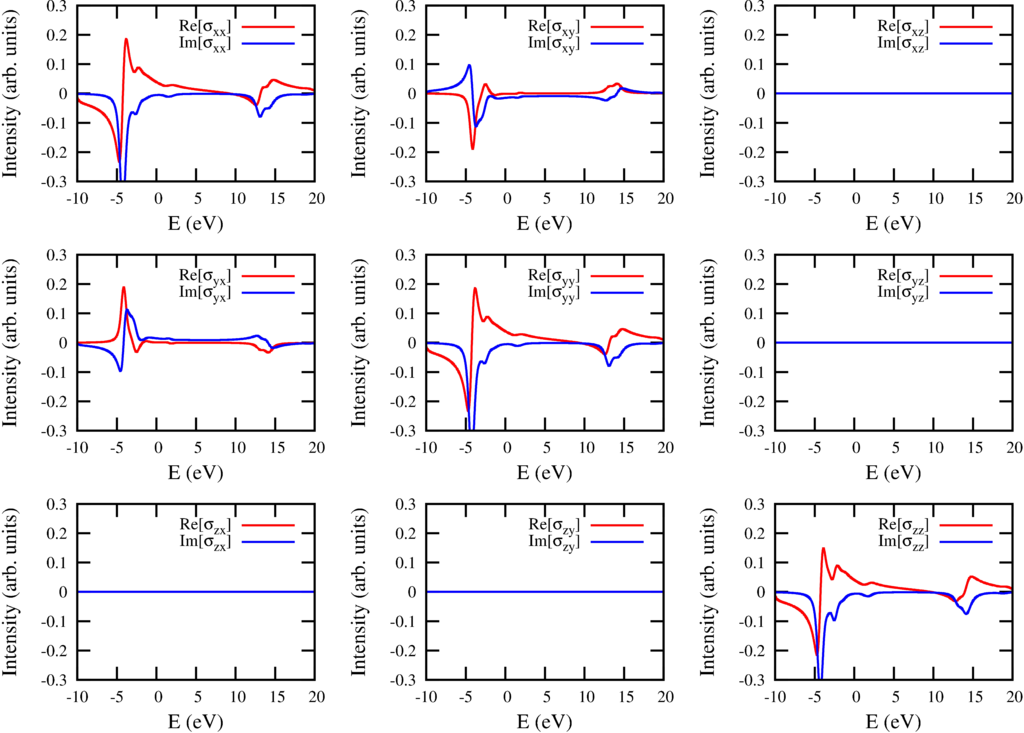 |
| $2p$ to $3d$ excitations for all possible polarizations represented as a conductivity tensor. Calculated using a block Lanczos method. |
|---|
The difference is:
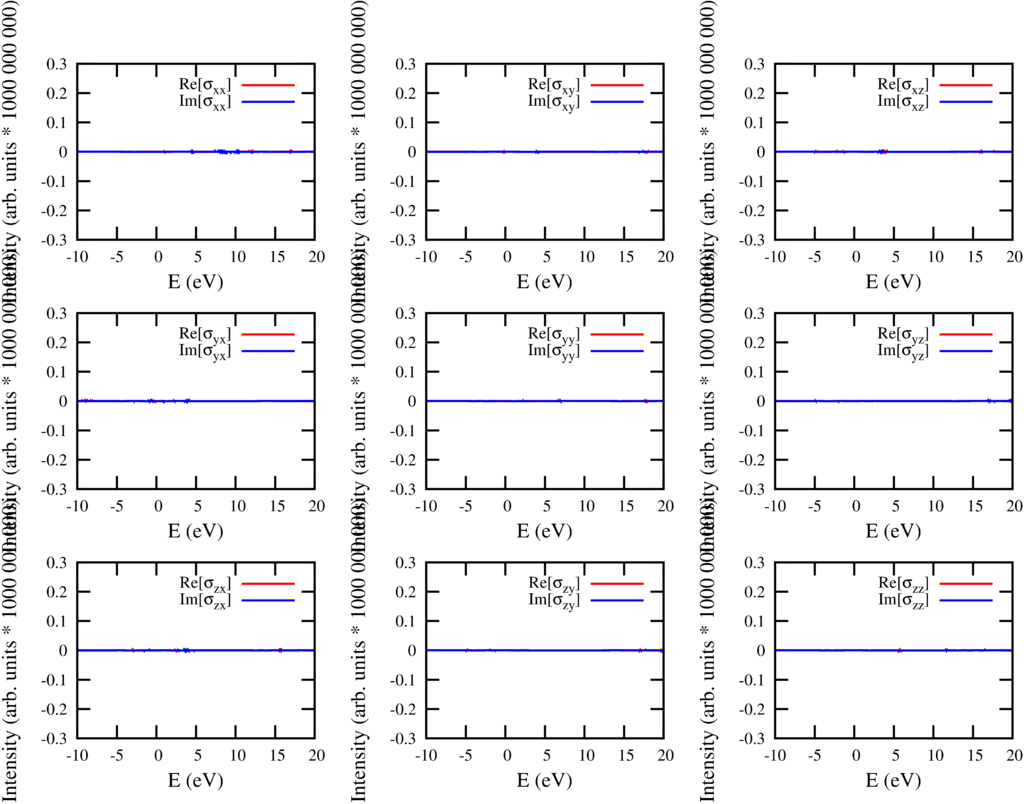 |
| Difference between the conductivity tensor calculated using method 1 or 2 |
|---|
The output of the script is:
- XAS_tensor.out
Start of BlockGroundState. Converge 3 states to an energy with relative variance smaller than 1.490116119384766E-06 Start of BlockOperatorPsiSerialRestricted Outer loop 1, Number of Determinants: 45 45 last variance 1.159112471523181E+00 Start of BlockOperatorPsiSerialRestricted Start of BlockGroundState. Converge 3 states to an energy with relative variance smaller than 1.490116119384766E-06 Start of BlockOperatorPsiSerial Outer loop 1, Number of Determinants: 32 100 last variance 8.359599622001442E+00 Start of BlockOperatorPsiSerial Outer loop 2, Number of Determinants: 100 138 last variance 1.315915512292445E+00 Start of BlockOperatorPsiSerial # <E> <S^2> <L^2> <J^2> <S_z^3d> <L_z^3d> <l.s> <F[2]> <F[4]> <Neg^3d> <Nt2g^3d><Neg^Ld> <Nt2g^Ld><N^3d> 1 -3.503 1.999 12.000 15.095 -0.908 -0.281 -0.305 -1.042 -0.924 2.186 5.990 3.825 6.000 8.175 2 -3.395 1.999 12.000 15.160 -0.004 -0.002 -0.322 -1.043 -0.925 2.189 5.988 3.823 6.000 8.178 3 -3.286 1.999 12.000 15.211 0.903 0.278 -0.336 -1.043 -0.925 2.193 5.987 3.820 6.000 8.180 Start of LanczosTriDiagonalizeRR Start of LanczosTriDiagonalizeRC Start of LanczosTriDiagonalizeRR Start of LanczosTriDiagonalizeRC Start of LanczosTriDiagonalizeRR Start of LanczosTriDiagonalizeRC Start of LanczosTriDiagonalizeRC Start of LanczosTriDiagonalizeRC Start of LanczosTriDiagonalizeRC Spectra printed to file: XASSigma_method1.dat Prepare gnuplot-file for Sigma Execute the gnuplot to produce plots and convert the output into a pdf-file Start of LanczosBlockTriDiagonalize Start of LanczosBlockTriDiagonalizeRC Spectra printed to file: XASSigma_method2.dat Prepare gnuplot-file for Sigma Execute the gnuplot to produce plots and convert the output into a pdf-file Spectra printed to file: XASSigma_diff.dat Prepare gnuplot-file for Sigma Execute the gnuplot to produce plots and convert the output into a pdf-file Timing results Total_time | NumberOfRuns | Running | Name 0:00:05 | 1 | 0 | Mehtod1 0:00:17 | 2 | 0 | Broaden 0:00:02 | 1 | 0 | Mehtod2
###