FY $L_{2,3}M_{1}$
In Fluoressence Yield spectroscopy one can focus on different decay channels. Each of them will yield a different spectrum. For a $2p$ to $3d$ excitation one can look at the $3s$ to $2p$ decay. The edge measured is thus the $L_{2,3}M_{1}$ edge.
The corresponding input file is:
- FY_L23M1.Quanty
-- in this example we calculate the fluorescence yield spectra for the L23M1 edge. -- i.e. we make an 2p to 3d excitation followed by a 3s to 2p decay. -- we minimize the output by setting the verbosity to 0 Verbosity(0) -- in order to do this calculation we need a Ni 2p shell a Ni 3s shell and a Ni 3d shell NF=18 NB=0 IndexDn_2p={0,2,4} IndexUp_2p={1,3,5} IndexDn_3s={6} IndexUp_3s={7} IndexDn_3d={8,10,12,14,16} IndexUp_3d={9,11,13,15,17} -- just like in the previous example we define several operators acting on the Ni -3d shell OppSx =NewOperator("Sx" ,NF, IndexUp_3d, IndexDn_3d) OppSy =NewOperator("Sy" ,NF, IndexUp_3d, IndexDn_3d) OppSz =NewOperator("Sz" ,NF, IndexUp_3d, IndexDn_3d) OppSsqr =NewOperator("Ssqr" ,NF, IndexUp_3d, IndexDn_3d) OppSplus=NewOperator("Splus",NF, IndexUp_3d, IndexDn_3d) OppSmin =NewOperator("Smin" ,NF, IndexUp_3d, IndexDn_3d) OppLx =NewOperator("Lx" ,NF, IndexUp_3d, IndexDn_3d) OppLy =NewOperator("Ly" ,NF, IndexUp_3d, IndexDn_3d) OppLz =NewOperator("Lz" ,NF, IndexUp_3d, IndexDn_3d) OppLsqr =NewOperator("Lsqr" ,NF, IndexUp_3d, IndexDn_3d) OppLplus=NewOperator("Lplus",NF, IndexUp_3d, IndexDn_3d) OppLmin =NewOperator("Lmin" ,NF, IndexUp_3d, IndexDn_3d) OppJx =NewOperator("Jx" ,NF, IndexUp_3d, IndexDn_3d) OppJy =NewOperator("Jy" ,NF, IndexUp_3d, IndexDn_3d) OppJz =NewOperator("Jz" ,NF, IndexUp_3d, IndexDn_3d) OppJsqr =NewOperator("Jsqr" ,NF, IndexUp_3d, IndexDn_3d) OppJplus=NewOperator("Jplus",NF, IndexUp_3d, IndexDn_3d) OppJmin =NewOperator("Jmin" ,NF, IndexUp_3d, IndexDn_3d) Oppldots=NewOperator("ldots",NF, IndexUp_3d, IndexDn_3d) -- as in the previous example we define the Coulomb interaction OppF0 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,0,1}) -- as in the previous example we define the crystal-field operator Akm = PotentialExpandedOnClm("Oh", 2, {0.6,-0.4}) OpptenDq = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- and as in the previous example we define operators that count the number of eg and t2g -- electrons Akm = PotentialExpandedOnClm("Oh", 2, {1,0}) OppNeg = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh", 2, {0,1}) OppNt2g = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- we need to define the core level spin-orbit interaction on the Ni 2p shell Oppcldots= NewOperator("ldots", NF, IndexUp_2p, IndexDn_2p) -- and the interaction between the Ni 2p shell and the Ni 3d shell OppUpdF0 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {1,0}, {0,0}) OppUpdF2 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,1}, {0,0}) OppUpdG1 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {1,0}) OppUpdG3 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {0,1}) -- next we define the dipole operator. The dipole operator is given as epsilon.r -- with epsilon the polarization vector of the light and r the unit position vector -- We can expand the position vector on (renormalized) spherical harmonics and use -- the crystal-field operator to create the dipole operator. -- we both define the dipole operator between the 2p and 3d shell as well as the dipole -- operator between the 3s and 2p shell -- x polarized light is defined as x = Cos[phi]Sin[theta] = sqrt(1/2) ( C_1^{(-1)} - C_1^{(1)}) Akm = {{1,-1,sqrt(1/2)},{1, 1,-sqrt(1/2)}} TXASx = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) T3s2px = NewOperator("CF", NF, IndexUp_2p, IndexDn_2p, IndexUp_3s, IndexDn_3s, Akm) -- y polarized light is defined as y = Sin[phi]Sin[theta] = sqrt(1/2) I ( C_1^{(-1)} + C_1^{(1)}) Akm = {{1,-1,sqrt(1/2)*I},{1, 1,sqrt(1/2)*I}} TXASy = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) T3s2py = NewOperator("CF", NF, IndexUp_2p, IndexDn_2p, IndexUp_3s, IndexDn_3s, Akm) -- z polarized light is defined as z = Cos[theta] = C_1^{(0)} Akm = {{1,0,1}} TXASz = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) T3s2pz = NewOperator("CF", NF, IndexUp_2p, IndexDn_2p, IndexUp_3s, IndexDn_3s, Akm) -- besides linear polarized light one can define circular polarized light as the sum of -- x and y polarizations with complex prefactors TXASr = sqrt(1/2)*(TXASx - I * TXASy) TXASl =-sqrt(1/2)*(TXASx + I * TXASy) -- we can remove zero's from the dipole operator by chopping it. TXASr.Chop() TXASl.Chop() -- once all operators are defined we can set some parameter values. -- the value of U drops out of a crystal-field calculation as the total number of electrons -- is always the same U = 0.000 -- F2 and F4 are often referred to in the literature as J_{Hund}. They represent the energy -- differences between different multiplets. Numerical values can be found in the back of -- my PhD. thesis for example. http://arxiv.org/abs/cond-mat/0505214 F2dd = 11.142 F4dd = 6.874 -- F0 is not the same as U, although they are related. Unimportant in crystal-field theory -- the difference between U and F0 is so important that I do include it here. (U=0 so F0 is not) F0dd = U+(F2dd+F4dd)*2/63 -- in crystal field theory U drops out of the equation, also true for the interaction between the -- Ni 2p and Ni 3d electrons Upd = 0.000 -- The Slater integrals between the 2p and 3d shell, again the numerical values can be found -- in the back of my PhD. thesis. (http://arxiv.org/abs/cond-mat/0505214) F2pd = 6.667 G1pd = 4.922 G3pd = 2.796 -- F0 is not the same as U, although they are related. Unimportant in crystal-field theory -- the difference between U and F0 is so important that I do include it here. (U=0 so F0 is not) F0pd = Upd + G1pd*1/15 + G3pd*3/70 -- tenDq in NiO is 1.1 eV as can be seen in optics or using IXS to measure d-d excitations tenDq = 1.100 -- the Ni 3d spin-orbit is small but finite zeta_3d = 0.081 -- the Ni 2p spin-orbit is very large and should not be scaled as theory is quite accurate here zeta_2p = 11.498 -- we can add a small magnetic field, just to get nice expectation values. (units in eV... ) Bz = 0.000001 -- the total Hamiltonian is the sum of the different operators multiplied with their prefactor Hamiltonian = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + tenDq*OpptenDq + zeta_3d*Oppldots + Bz*(2*OppSz+OppLz) -- We normally do not include core-valence interactions between filed and partially filled -- shells as it drops out anyhow. For the XAS we thus need to define a "different" -- (more complete) Hamiltonian. XASHamiltonian = Hamiltonian + zeta_2p * Oppcldots + F0pd * OppUpdF0 + F2pd * OppUpdF2 + G1pd * OppUpdG1 + G3pd * OppUpdG3 -- We saw in the previous example that NiO has a ground-state doublet with occupation -- t2g^6 eg^2 and S=1 (S^2=S(S+1)=2). The next state is 1.1 eV higher in energy and thus -- unimportant for the ground-state upto temperatures of 10 000 Kelvin. We thus restrict -- the calculation to the lowest 3 eigenstates. Npsi=3 -- We need a filling of 6 electrons in the 2p shell -- 2 electrons in the 3s shell -- and 8 electrons in the 3d shell StartRestrictions = {NF, NB, {"111111 11 0000000000",8,8}, {"000000 00 1111111111",8,8}} -- And calculate the lowest 3 eigenfunctions psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi) -- In order to get some information on these eigenstates it is good to plot expectation values -- We first define a list of all the operators we would like to calculate the expectation value of oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSz, OppLz, Oppldots, OppF2, OppF4, OppNeg, OppNt2g}; -- next we loop over all operators and all states and print the expectation value print(" <E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g>"); for i = 1,#psiList do for j = 1,#oppList do expectationvalue = Chop(psiList[i]*oppList[j]*psiList[i]) io.write(string.format("%6.3f ",Complex.Re(expectationvalue))) end io.write("\n") end -- here we calculate the x-ray absorption spectra, not the main task of this file, but nice to do so we can compare XASSpectra = CreateSpectra(XASHamiltonian, {TXASz, TXASr, TXASl}, psiList, {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}); XASSpectra.Print({{"file","FYL23M1_XAS.dat"}}); -- and we calculate the FY spectra FYSpectra = CreateFluorescenceYield(XASHamiltonian, {TXASz, TXASr, TXASl}, {T3s2px, T3s2py, T3s2pz}, psiList, {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) FYSpectra.Print({{"file","FYL23M1_Spec.dat"}}) -- in order to plot both the XAS and FY spectra we can define a gnuplot script gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set style line 2 lt 1 lw 1 lc rgb "#FF0000" set style line 3 lt 1 lw 1 lc rgb "#00FF00" set style line 4 lt 1 lw 1 lc rgb "#0000FF" set xlabel "E (eV)" font "Times,10" set ylabel "Intensity (arb. units)" font "Times,10" set out 'FYL23M1.ps' set terminal postscript portrait enhanced color "Times" 8 size 7.5,6 set yrange [0:0.6] set size 1,1 set multiplot layout 3, 3 plot "FYL23M1_XAS.dat" u 1:(-$3 ) title 'z-polarized Sz=-1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$2) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$4) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$6) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$5 ) title 'z-polarized Sz= 0' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$8) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$10) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$12) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$7 ) title 'z-polarized Sz= 1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$14) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$16) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$18) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$9 ) title 'r-polarized Sz=-1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$20) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$22) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$24) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$11) title 'r-polarized Sz= 0' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$26) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$28) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$30) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$13) title 'r-polarized Sz= 1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$32) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$34) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$36) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$15) title 'l-polarized Sz=-1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$38) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$40) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$42) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$17) title 'l-polarized Sz= 0' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$44) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$46) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$48) title 'FY - z out' with lines ls 4 plot "FYL23M1_XAS.dat" u 1:(-$19) title 'l-polarized Sz= 1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M1_Spec.dat" u 1:(4*$50) title 'FY - x out' with lines ls 2,\ "FYL23M1_Spec.dat" u 1:(4*$52) title 'FY - y out' with lines ls 3,\ "FYL23M1_Spec.dat" u 1:(4*$54) title 'FY - z out' with lines ls 4 unset multiplot ]] -- write the gnuplot script to a file file = io.open("FYL23M1.gnuplot", "w") file:write(gnuplotInput) file:close() -- call gnuplot to execute the script os.execute("gnuplot FYL23M1.gnuplot") -- and change the ps to pdf and eps os.execute("ps2pdf FYL23M1.ps ; ps2eps FYL23M1.ps ; mv FYL23M1.eps temp.eps ; eps2eps temp.eps FYL23M1.eps ; rm temp.eps")
The resulting spectra are: (for a description see the text for the $L_{2,3}M_{45}$ spectra.
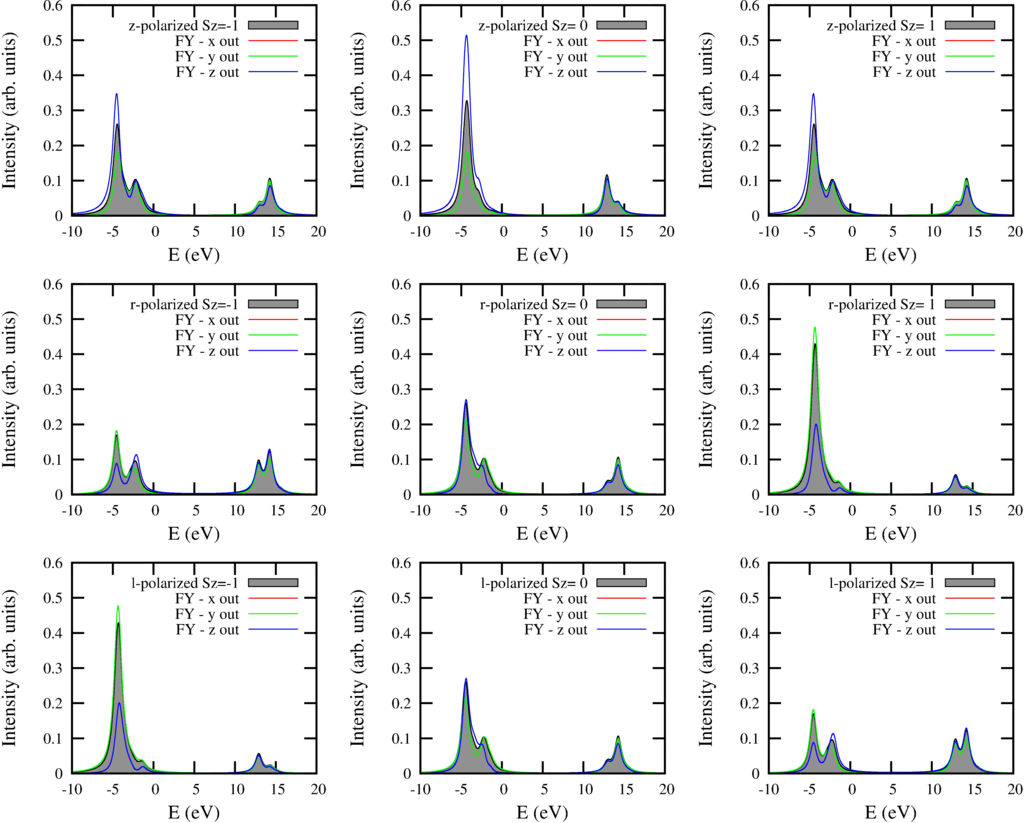
And the text output is:
- FY_L23M1.out
<E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g> -2.721 1.999 12.000 15.120 -0.994 -0.286 -0.324 -1.020 -0.878 2.011 5.989 -2.721 1.999 12.000 15.120 -0.000 -0.000 -0.324 -1.020 -0.878 2.011 5.989 -2.721 1.999 12.000 15.120 0.994 0.286 -0.324 -1.020 -0.878 2.011 5.989 Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR