Table of Contents
This is an old revision of the document!
Orientation Z
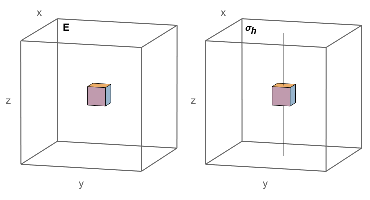
Symmetry Operations
In the Cs Point Group, with orientation Z there are the following symmetry operations
| Operator | Orientation |
|---|---|
| $\text{E}$ | $\{0,0,0\}$ , |
| $\sigma _h$ | $\{0,0,1\}$ , |
Different Settings
Character Table
| $ $ | $ \text{E} \,{\text{(1)}} $ | $ \sigma_h \,{\text{(1)}} $ |
|---|---|---|
| $ \text{A'} $ | $ 1 $ | $ 1 $ |
| $ \text{A''} $ | $ 1 $ | $ -1 $ |
Product Table
| $ $ | $ \text{A'} $ | $ \text{A''} $ |
|---|---|---|
| $ \text{A'} $ | $ \text{A'} $ | $ \text{A''} $ |
| $ \text{A''} $ | $ \text{A''} $ | $ \text{A'} $ |
Sub Groups with compatible settings
Super Groups with compatible settings
Invariant Potential expanded on renormalized spherical Harmonics
Any potential (function) can be written in spherical coordinates as a sum over spherical harmonics $$V(\vec{r}) = \sum_{k=0}^{\infty} \sum_{m=-k}^{k} A_{k,m}(r) C^{(m)}_k(\theta,\phi)$$. With $C^{(m)}_k(\theta,\phi)$ a renormalised spherical harmonics $C^{(m)}_k(\theta,\phi)=\sqrt{\frac{4\pi}{2k+1}}Y^{(m)}_k(\theta,\phi)$. The allowed expansion coefficients $A_{k,m}(r)$, or once evaluated for a given radial wave-function $A_{k,m}=\langle\psi(r)|A_{k,m}(r)|\psi(r)\rangle$, such that $V(\vec{r}) is invariant under all symmetry operations of the Cs Point group with orientation Z are:
Input format suitable for Mathematica (Quanty.nb)
$$A_{k,m} = \begin{cases} A(0,0) & k=0\land m=0 \\ -A(1,1)+i \text{Ap}(1,1) & k=1\land m=-1 \\ A(1,1)+i \text{Ap}(1,1) & k=1\land m=1 \\ A(2,2)-i \text{Ap}(2,2) & k=2\land m=-2 \\ A(2,0) & k=2\land m=0 \\ A(2,2)+i \text{Ap}(2,2) & k=2\land m=2 \\ -A(3,3)+i \text{Ap}(3,3) & k=3\land m=-3 \\ -A(3,1)+i \text{Ap}(3,1) & k=3\land m=-1 \\ A(3,1)+i \text{Ap}(3,1) & k=3\land m=1 \\ A(3,3)+i \text{Ap}(3,3) & k=3\land m=3 \\ A(4,4)-i \text{Ap}(4,4) & k=4\land m=-4 \\ A(4,2)-i \text{Ap}(4,2) & k=4\land m=-2 \\ A(4,0) & k=4\land m=0 \\ A(4,2)+i \text{Ap}(4,2) & k=4\land m=2 \\ A(4,4)+i \text{Ap}(4,4) & k=4\land m=4 \\ -A(5,5)+i \text{Ap}(5,5) & k=5\land m=-5 \\ -A(5,3)+i \text{Ap}(5,3) & k=5\land m=-3 \\ -A(5,1)+i \text{Ap}(5,1) & k=5\land m=-1 \\ A(5,1)+i \text{Ap}(5,1) & k=5\land m=1 \\ A(5,3)+i \text{Ap}(5,3) & k=5\land m=3 \\ A(5,5)+i \text{Ap}(5,5) & k=5\land m=5 \\ A(6,6)-i \text{Ap}(6,6) & k=6\land m=-6 \\ A(6,4)-i \text{Ap}(6,4) & k=6\land m=-4 \\ A(6,2)-i \text{Ap}(6,2) & k=6\land m=-2 \\ A(6,0) & k=6\land m=0 \\ A(6,2)+i \text{Ap}(6,2) & k=6\land m=2 \\ A(6,4)+i \text{Ap}(6,4) & k=6\land m=4 \\ A(6,6)+i \text{Ap}(6,6) & k=6\land m=6 \end{cases}$$
Input format suitable for Quanty
Akm = {{0, 0, A(0,0)} ,
{1,-1, (-1)*(A(1,1)) + ((+1*I))*(Ap(1,1))} ,
{1, 1, A(1,1) + ((+1*I))*(Ap(1,1))} ,
{2, 0, A(2,0)} ,
{2,-2, A(2,2) + ((+-1*I))*(Ap(2,2))} ,
{2, 2, A(2,2) + ((+1*I))*(Ap(2,2))} ,
{3,-1, (-1)*(A(3,1)) + ((+1*I))*(Ap(3,1))} ,
{3, 1, A(3,1) + ((+1*I))*(Ap(3,1))} ,
{3,-3, (-1)*(A(3,3)) + ((+1*I))*(Ap(3,3))} ,
{3, 3, A(3,3) + ((+1*I))*(Ap(3,3))} ,
{4, 0, A(4,0)} ,
{4,-2, A(4,2) + ((+-1*I))*(Ap(4,2))} ,
{4, 2, A(4,2) + ((+1*I))*(Ap(4,2))} ,
{4,-4, A(4,4) + ((+-1*I))*(Ap(4,4))} ,
{4, 4, A(4,4) + ((+1*I))*(Ap(4,4))} ,
{5,-1, (-1)*(A(5,1)) + ((+1*I))*(Ap(5,1))} ,
{5, 1, A(5,1) + ((+1*I))*(Ap(5,1))} ,
{5,-3, (-1)*(A(5,3)) + ((+1*I))*(Ap(5,3))} ,
{5, 3, A(5,3) + ((+1*I))*(Ap(5,3))} ,
{5,-5, (-1)*(A(5,5)) + ((+1*I))*(Ap(5,5))} ,
{5, 5, A(5,5) + ((+1*I))*(Ap(5,5))} ,
{6, 0, A(6,0)} ,
{6,-2, A(6,2) + ((+-1*I))*(Ap(6,2))} ,
{6, 2, A(6,2) + ((+1*I))*(Ap(6,2))} ,
{6,-4, A(6,4) + ((+-1*I))*(Ap(6,4))} ,
{6, 4, A(6,4) + ((+1*I))*(Ap(6,4))} ,
{6,-6, A(6,6) + ((+-1*I))*(Ap(6,6))} ,
{6, 6, A(6,6) + ((+1*I))*(Ap(6,6))} }
One particle coupling on a basis of spherical harmonics
Rotation matrix to symmetry adapted functions (choice is not unique)
One particle coupling on a basis of symmetry adapted functions
Potential for s orbitals
Potential for p orbitals
Potential for d orbitals
Potential for f orbitals
Potential for s-p orbital mixing
Potential for s-d orbital mixing
Potential for s-f orbital mixing
Potential for p-d orbital mixing
Potential for p-f orbital mixing
Potential for d-f orbital mixing
Table of several point groups
Return to Main page on Point Groups
| Nonaxial groups | C1 | Cs | Ci | ||||
|---|---|---|---|---|---|---|---|
| Cn groups | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| Dn groups | D2 | D3 | D4 | D5 | D6 | D7 | D8 |
| Cnv groups | C2v | C3v | C4v | C5v | C6v | C7v | C8v |
| Cnh groups | C2h | C3h | C4h | C5h | C6h | ||
| Dnh groups | D2h | D3h | D4h | D5h | D6h | D7h | D8h |
| Dnd groups | D2d | D3d | D4d | D5d | D6d | D7d | D8d |
| Sn groups | S2 | S4 | S6 | S8 | S10 | S12 | |
| Cubic groups | T | Th | Td | O | Oh | I | Ih |
| Linear groups | C$\infty$v | D$\infty$h |